OmegaKV
- 22
- 1
I want to the line integral in the following picture:
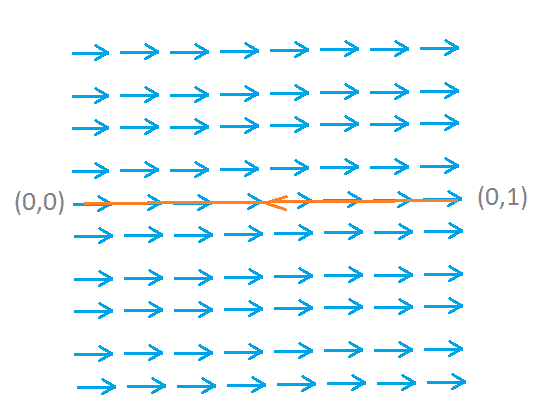
The field is the blue arrows that go left to right, and the path is the orange line that is going from right to left.
Just by looking at the picture, it is clear that the result will be negative, but when I set up the integration this is what I get:
I'm letting the field be:
f(x)=\hat{x}
and since the path is pointing left, ds will be:
ds=dx*(-\hat{x})=-dx\hat{x}
and the path goes from x=1 to x=0, so the integration limits are from 1 to 0.
so the line integral is:
\int^b_a f \cdot ds=\int^0_1 (\hat{x} \cdot (-dx\hat{x})) = \int^0_1 (-dx) = 1
Why am I getting a positive number?
The field is the blue arrows that go left to right, and the path is the orange line that is going from right to left.
Just by looking at the picture, it is clear that the result will be negative, but when I set up the integration this is what I get:
I'm letting the field be:
f(x)=\hat{x}
and since the path is pointing left, ds will be:
ds=dx*(-\hat{x})=-dx\hat{x}
and the path goes from x=1 to x=0, so the integration limits are from 1 to 0.
so the line integral is:
\int^b_a f \cdot ds=\int^0_1 (\hat{x} \cdot (-dx\hat{x})) = \int^0_1 (-dx) = 1
Why am I getting a positive number?