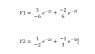Solving Matrix Differential Equations: How to Obtain the X Matrix

[zack7]

Homework Statement

The questions are in the image

The Attempt at a Solution

My solutions are
V1=3*(1 -2)e^-2t+ (-2) (1 -3)e^-3t
V2=1*(1 -2)e^-2t+ (-1) (1 -3)e^-3t

How do I get the X matrix since my solutions are in exponential still.

Thank you for all the help

 

[Some Pig]

According to your solution,
$$X=(v_1\ v_2)=\begin{pmatrix}3e^{-2t}-2e^{-3t}&-6e^{-2t}+6e^{-3t}\\<br /> e^{-2t}-e^{-3t}&-2e^{-2t}+3e^{-3t}\end{pmatrix}.$$

 

[zack7]

According to your solution,
$$X=(v_1\ v_2)=\begin{pmatrix}3e^{-2t}-2e^{-3t}&-6e^{-2t}+6e^{-3t}\\<br /> e^{-2t}-e^{-3t}&-2e^{-2t}+3e^{-3t}\end{pmatrix}.$$

That means I just plug in t=0 to prove that x(0)=(1 0
0 1) and also use the same method to prove that dx/dt =AX

 

[vela]

You have the columns and rows swapped.

 

[zack7]

You have the columns and rows swapped.

Even after multiplying it I get this respective solutions, what do I do next?

 

[vela]

You can write v₁ as a single vector:
$$\vec{v}_1 = \begin{pmatrix} 3e^{-2t} - 2e^{-3t} \\ -6e^{-2t} + 6e^{-3t}\end{pmatrix}$$Do the same for $\vec{v}_2$.

 

[zack7]

You can write v₁ as a single vector:
$$\vec{v}_1 = \begin{pmatrix} 3e^{-2t} - 2e^{-3t} \\ -6e^{-2t} + 6e^{-3t}\end{pmatrix}$$Do the same for $\vec{v}_2$.

i get that part but after that what do I do to get just numbers in my 2x2 matrix so that I can prove dx/dt =AX and x(0)= \begin{pmatrix}1 0\\ 0 1\end{pmatrix}

 

[vela]

Like the problem says, the first column of X is v₁. Its second column is v₂. It's not going to be just numbers. I'm not sure why you think it has to be.

 

[zack7]

Like the problem says, the first column of X is v₁. Its second column is v₂. It's not going to be just numbers. I'm not sure why you think it has to be.

Okay but then if I put t=0 into the x equation, I do not get the identity matrix and how would I verify that dx/dt=AX by just differentiating the X matrix?.

Thank you for all the help

 

[vela]

Show us how you're calculating X when t=0.

 

[zack7]

Show us how you're calculating X when t=0.

Okay I got just did a arithmetic error, but how do I verify that dx/dt=AX

 

[vela]

Calculate both sides and show they're equal to each other.

 

[zack7]

Okay I will give it a try, thank you very much for all the help.