kushan
- 256
- 0
Hello everybody ,
I am stuck at this question ,
,
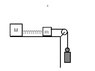
Two blocks of masses m=1kg and M =2kg are connected by a non-deformed light spring .They are lying on a rough horizontal surface . The coefficient of friction is 0.4 ,What minimun constant force has to be applied in the horizontal direction to the block m , in order to shift the order block M .
I came up with work energy conservation theorem
F.x = 1/2 kx^2 +f1.x + 1/2mv^2
(where F is external force
f1is force of friction on m. and v is velocity of mass m)
F-kx-f1=ma1
and when block M is just about to move kx=f2
(here f2 is force of friction on M
, its leading me nowhere .
Any help?
I am stuck at this question
Homework Statement
Two blocks of masses m=1kg and M =2kg are connected by a non-deformed light spring .They are lying on a rough horizontal surface . The coefficient of friction is 0.4 ,What minimun constant force has to be applied in the horizontal direction to the block m , in order to shift the order block M .
Homework Equations
I came up with work energy conservation theorem
F.x = 1/2 kx^2 +f1.x + 1/2mv^2
(where F is external force
f1is force of friction on m. and v is velocity of mass m)
F-kx-f1=ma1
and when block M is just about to move kx=f2
(here f2 is force of friction on M
, its leading me nowhere .
Any help?