charrotrust
- 2
- 0
- Homework Statement
- Mutual Induction
- Relevant Equations
- L=Φ/I
hello PF. I have this exercise to do but I don't know how to do it.
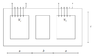
Let's assume that the core in the figure is made up of ferromagnetic permeability material
μ = 2000 μ0. Let a = 4 cm, b = 2 cm, c = 3 cm the geometric dimensions, S = 8 cm2 the section
transversal, N1 = 100, N2 = 300 the number of turns of the two windings.
• Calculate the inductances of the two windings and the mutual inductances between
same;
• the position of the dots needed to identify the sign of the mutual is established
inductance;
• if two currents I1 = 3 A, I2 = 4 A flow in the two windings, both entering
on the side of the dots, calculate the overall flow concatenated with the two
windings.
Let's assume that the core in the figure is made up of ferromagnetic permeability material
μ = 2000 μ0. Let a = 4 cm, b = 2 cm, c = 3 cm the geometric dimensions, S = 8 cm2 the section
transversal, N1 = 100, N2 = 300 the number of turns of the two windings.
• Calculate the inductances of the two windings and the mutual inductances between
same;
• the position of the dots needed to identify the sign of the mutual is established
inductance;
• if two currents I1 = 3 A, I2 = 4 A flow in the two windings, both entering
on the side of the dots, calculate the overall flow concatenated with the two
windings.