Lijnk
- 4
- 0
I'm having problems with an n-body simulator. I tried to use the gravitational equation for vectors, however that didn't exactly work, so I split up the forces into their respective X and Y components and used two separate gravitational equations. The problem is the entire body is exploding rather than coming in. I'm obviously doing something wrong with the gravity, I'm just not sure what it is.
I can answer any questions about the code or make it more verbose if needed.
The equation I'm basing it off of is two of these. One for the X value and the other for the Y.
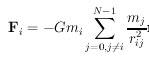
(ignore the last right bracket looking thing. The original equation was the vector one, but the one I'm using doesn't need the unit vector.)
Code:
void forceInit() //Initializes/Updates the forces acting on each particle from the other particles
{
int i, j;
double rx=0, ry=0, r1, r2;
for(i=0;i<N;i++) //N is the number of particles
{
for(j=0;j<N;j++)
{
if(j==i) continue; //so we don't check the particle against itself
rx += pow(part[0][j] - part[0][i], 2);
ry += pow(part[1][j] - part[1][i], 2);
}
r1 = pow(rx, -1); //converts to 1/r since all particle masses are =1
r2 = pow(ry, -1);
part[2][i]=G*r1; //G is gravitational constant
part[3][i]=G*r2;
rx = 0;
ry = 0;
}
}
void forceNext() //Converts the force into the next location for the particle
{
int i;
forceInit();
for(i=0;i<N;i++)
{
part[4][i] += part[2][i] * T; //T is the change in time
part[5][i] += part[3][i] * T;
part[0][i] += part[4][i] * T;
part[1][i] += part[5][i] * T;
}
}
/*part[x][y] is an array listing all the particle's properties
x is the property type and y is the particle number
property types:
0 - X coordinate
1 - Y coordinate
2 - X force
3 - Y force
4 - X Velocity
5 - Y Velocity
6 - Theta (used for initial velocity and position)
*/I can answer any questions about the code or make it more verbose if needed.
The equation I'm basing it off of is two of these. One for the X value and the other for the Y.
(ignore the last right bracket looking thing. The original equation was the vector one, but the one I'm using doesn't need the unit vector.)