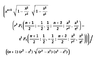Solving One Tough Integral: Elliptical Integrals and Inverse Jacobian Functions

[pocaracas]

Hi,

I've been dealing with a really mind buster, at least, for me.
Here it is
$$I_n(r,z)=\int_z^r\frac{p^n}{\sqrt{r^2-p^2}\sqrt{p^2-z^2}}\,dp$$

where $$n$$ is an integer and $$0<z<r<1$$.

Mathematica tells me that the result is zero, but I'd like to know how to get there.
I've thought about elliptical integrals but Abramowitz doesn't help much beyond telling me that the Equivalent Inverse Jacobian Elliptic Function of
$$a\int_b^x\frac{dt}{\sqrt{(a^2-t^2)(t^2-b^2)}}$$
is
$$nd^{-1}\left(\frac{x}{b}|\frac{a^2-b^2}{a^2}\right)$$

and
$$a\int_x^a\frac{dt}{\sqrt{(a^2-t^2)(t^2-b^2)}}$$
is
$$dn^{-1}\left(\frac{x}{a}|\frac{a^2-b^2}{a^2}\right)$$

Whatever this means. I know nothing about these functions. nd and dn?
Any help?

 

[Mute]

It says the result is zero for any choice of n, r and z? That's certainly not true! Just pick some values and plot the integrand, e.g. n = 3, r = 2, z = 1. You'll see that in this example from 1 to 2 the integrand is only positive, and hence the integral can't be zero.

I'm assuming then that I misinterpreted the question. I doubt I can help you beyond what I pointed out there above, but reclarifying the question might help others see what your problem is.

 

[Gib Z]

Mute, look at the inequality condition on z and r.

I'm not sure if that's do able in terms of elementary functions, especially since it's the inverse of an elliptic function. Must it be solved analytically?

 

[Mute]

Mute, look at the inequality condition on z and r.

Doesn't really matter. r = 0.9 and z = 0.5 still gives a nonzero result when graphed, which is what I was getting at. We need to be given more information about what the problem is, because it's not clear under what conditions the integral is zero.

I'm not sure if that's do able in terms of elementary functions, especially since it's the inverse of an elliptic function. Must it be solved analytically?

I remember the book on Solitons by Drazin and Johnson had some discussion of these functions since some of them were solutions to the KdV equation, but I can't remember to what extent the functions were discussed (since it is primarily a book about the KdV equations and Solitons(, so the book might not be so usefull for this purposes. At any rate, the book at Amazon is

https://www.amazon.com/dp/0521336554/?tag=pfamazon01-20

 

[chandranshu]

Result of the integral

Hi,

Solving the integral as an indefinite integral results in a nice little function involving hypergeometric functions. Please find the result in the attached GIF file.

I guess it'll be easy now for everyone to evaluate it for all the values of r and z.

Regards
Chandranshu

 

[chandranshu]

Missing information

I forgot to add that the hypergeometric function in the result set is the Appell Hypergeometric function of two variables. See http://mathworld.wolfram.com/AppellHypergeometricFunction.html for more information. Also, I have used 'x' as the variable of integration in place of 'p'. This should be a small inconvenience.

Regards
Chandranshu