Solving Partial Derivatives with f(x-z)=x+y+z

[imana41]

hi i have a problem for this
if f(x-z)=x+y+z solve

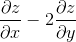
can i say u=x-z and write F(x,y,z)=x+y+z-f(u) and then

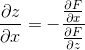
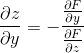
or this isn't true ? thanks if u help me.

 

[lanedance]

f(x-z)=x+y+z, this doesn't make sense, the way you've written it f is a function of one variable (x-z), but has 3 variables and does not reference the original variable (x-z)

 

[imana41]

what should i do ?

 

[lanedance]

can you start by trying to write the question exactly as it was written?

 

[HallsofIvy]

For example, are you given that f(x, y, z)= x+ y+ z= 0?

 

[imana41]

For example, are you given that f(x, y, z)= x+ y+ z= 0?

no jus written f(x-z)=x+y+z and f is a function of x and y(x,y are Independent)