Solving Pulley & Block Problems: Acceleration of A

[chenying]

Homework Statement

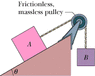
Body A in Fig. 6-36 weighs 102 N, and body B weighs 32 N. The coefficients of friction between A and the incline are μs = .56 and μk = 0.25. Angle θ is 40°. Let the positive direction of an x-axis be down the slope. What is the acceleration of A if A is initially (a) at rest, (b) moving up the incline, and (c) moving down the incline?

(see the attachment)

Homework Equations

$$\Sigma$$F = ma

Frictional force = F$$_{k}$$ = $$\mu$$$$_{k}$$ * F$$_{N}$$

T = tension in string

The Attempt at a Solution

for a, I know the answer is 0 because the block is at rest, therefore it will remain at rest until another force acts on it.

Now for b, I stated that the sum of all forces on the block would equal m*-a, a being negative because the problem stated the coordinate axes. So

$$\Sigma$$F = ma

mgsin$$\Theta$$ - F$$_{s}$$ + T = m*-a

the F$$_{s}$$ should be F$$_{k}$$

plugging the numbers in and solving for a, i get a value of 7.5 /s^2, which is wayyyyy too fast. I do not know what is wrong with my set up, so can anyone help me out?

 

[ehild]

When the body A moves upwards (negative direction) the friction points downwards as it acts against the motion. The tension is negative as its acts uphill. The resultant force points downwards, and so does the acceleration: it is positive.
Do not assume sign for the acceleration, you will get it from the solution. Newton's second law states F=ma, both F and a vectors. ehild