Solving Retarded Potentials Homework: Electric & Magnetic Fields

[stunner5000pt]

Homework Statement

Suppose a wire carries a current such taht
I(t) = 0 for t< = 0
= k t for t > 0
Find the electric and magnetic fields generated

2. The attempt at a solution
trying to figure out vector potential first
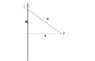
looking at the diagram
s is the distance fro a point P to the wire which is positioned on the Z axis.
r' is the distance to some section of the wire dz

the only contribution is for t > s/c, otherwise the em fields haven't reached the point P

we only need to integrate along the z since there is X and Y symmetry

$$z = \pm \sqrt{c^2 t^2 - s^2}$$
but we are going to get the EM fields from time $= t - r' / c = t - \frac{\sqrt{z^2 + s^2}}{c}$

so we're lookign at integrating this

$$A = \frac{\mu_{0}}{4 \pi} 2 \int_{0}^{\sqrt{c^2 t^2 - s^2}} \frac{k (t-\frac{\sqrt{z^2 + s^2}}{c}}{\sqrt{z^2 + s^2}} dz$$

ahve i gone wrong somewhere??

something wrong in my logic?

please help!

thanks for any and all input!

 

[stunner5000pt]

bump

 

[siddharth]

$$A = \frac{\mu_{0}}{4 \pi} 2 \int_{0}^{\sqrt{c^2 t^2 - s^2}} \frac{k (t-\frac{\sqrt{z^2 + s^2}}{c}}{\sqrt{z^2 + s^2}} dz$$

That looks correct to me