Solving Rotating Ice Skaters Problem: Is their Straight Line Parallel?

[brotherbobby]

Statement of the problem :
Two ice skaters circle about a point while holding hands. At a certain moment both let go and move along straight lines. Are the two straight lines parallel? Explain.

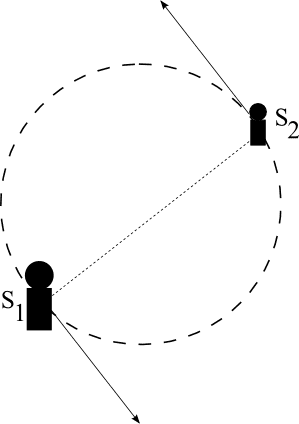
My attempt : Calling the two ice skaters $S_1$ and $S_2$, they must lie along the same line passing through the centre of the circle at all points. That implies, despite their different masses, they must rotate with the same (linear) velocity $v$. When they separate, they should move in lines that are tangent to the circle and therefore perpendicular to the diameter to which they were "connected" last. Hence their straight lines must be parallel.

Doubts :

1. The problem is one on angular momentum $(\mathbf L = \mathbf r \times \mathbf p)$ and its conservation. I haven't used any of that in my solution, even if I am correct.

2. If the masses $(m_1 \neq m_2)$ are different, should their linear speeds $(v_1, v_2)$ and radii $(r_1, r_2)$ by the same? Of course, both could be different in a way such that their angular speed $(\omega = \frac{v}{r})$ remains the same.

 

[haruspex]

To answer this question at all, I think you have to pretend there are no horizontal forces between ice and skaters.

The problem is one on angular momentum

Not obvious to me how you would use that here. You could use conservation of linear momentum. What is the linear momentum of the system before they decouple?

If the masses (m1≠m2)(m1≠m2)(m_1 \neq m_2) are different, should their linear speeds (v1,v2)(v1,v2)(v_1, v_2) and radii (r1,r2)(r1,r2)(r_1, r_2) by the same?

Certainly the diagram looks like they are unequal.
Would the radii be the same? Think about the centripetal force on each. What must be the same is the angular velocity.

 

[brotherbobby]

Not obvious to me how you would use that here. You could use conservation of linear momentum. What is the linear momentum of the system before they decouple?

The total linear momentum of the system before they decouple is zero [$p_{total} = 0$].

Would the radii be the same? Think about the centripetal force on each. What must be the same is the angular velocity.

Yes, the problem is, the radii have to be the same, as the problem states : "two skaters circle about a point". Hence the centripetal force on each will have to be different, if their masses are unequal. ($F_i = m_i \omega^2 r$)

I paste below a sketch of my solution to the problem. My conclusion is that both the skaters would move away in lines with the same speed in opposite direction, the lines being parallel.

Thank you for your interest.

 

[haruspex]

the radii have to be the same, as the problem states : "two skaters circle about a point".

They can each circle about the same point but at different radii. Indeed, if different masses that is what they must do.

 

[phinds]

They can each circle about the same point but at different radii. Indeed, if different masses that is what they must do.

 

[brotherbobby]

They can each circle about the same point but at different radii. Indeed, if different masses that is what they must do.

Yes, that is what happens for a pair of (binary) stars. The problem is, the two skaters "circle about a point while holding hands".

If they revolved about their CM, their relative distance ($r = r_1-r_2$) will change. That is not possible if they are holding hands.

I believe this is a simpler problem than the binary-star problem.

Thank you for your interest and time.

 

[jbriggs444]

If they revolved about their CM, their relative distance ($r = r_1-r_2$) will change.

Can you explain why you think so? Also their distance from one another is equal to $r_1+r_2$ surely.

 

[haruspex]

the two skaters "circle about a point while holding hands".

I don't see the difficulty.
Draw the two skaters as point masses. Put the CoM somewhere between them. Draw a line through the CoM, connecting the skaters, to represent their arms. Pick some point on that line, need not be the CoM, to represent their clasped hands.
Each circles around the CoM.