cde42003
- 22
- 0
I have a couple of questions.
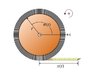
1. Assume that the function x(t) represents the length of tape that has unwound as a function of time. Find theta(t), the angle through which the drum will have rotated, as a function of time.
Express your answer (in radians) in terms of x(t) and any other given quantities.
There is a picture for this that I attached below. This question doesn't seem very difficult but I cannot think of a way to solve it. I know that the amount of tape unwound in one revolution is 2*pi*r but do not know how to relate this to x(t)
2. A magnetic computer disk 8.0 cm in diameter is initially at rest. A small dot is painted on the edge of the disk. The disk accelerates at 600 rad/s^2 for .5s, then coasts at a steady angular velocity for another .5s.
A.What is the speed of the dot at t = 1.0 s? This equals 12m/s
b. Through how many revolutions has it turned? This is the problem. I would think that you should find circumference of the circle and use the speed from part a to find the number of revolutions but this has not worked.
Any help would be greatly appreciated. Thanks
1. Assume that the function x(t) represents the length of tape that has unwound as a function of time. Find theta(t), the angle through which the drum will have rotated, as a function of time.
Express your answer (in radians) in terms of x(t) and any other given quantities.
There is a picture for this that I attached below. This question doesn't seem very difficult but I cannot think of a way to solve it. I know that the amount of tape unwound in one revolution is 2*pi*r but do not know how to relate this to x(t)
2. A magnetic computer disk 8.0 cm in diameter is initially at rest. A small dot is painted on the edge of the disk. The disk accelerates at 600 rad/s^2 for .5s, then coasts at a steady angular velocity for another .5s.
A.What is the speed of the dot at t = 1.0 s? This equals 12m/s
b. Through how many revolutions has it turned? This is the problem. I would think that you should find circumference of the circle and use the speed from part a to find the number of revolutions but this has not worked.
Any help would be greatly appreciated. Thanks