Solving Student's Ladder Homework Problem

[ledphones]

Homework Statement

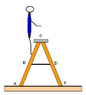
A student is standing on a ladder as shown in the figure to the right. Each leg of the ladder is 2.6 m long and is hidged at point C. The tie-rod (BD) attached halfway up and is 0.79 m long. The student is standing at a spot 1.95 m along the leg and her weight is 510 N. (You may ignore the weight of the ladder and any minor friction between the floor and the legs.)

a) What is the tension in the tie-rod?
TR = N

b) What is the vertical component of the force of the ground on the ladder leg at point A?

c) What is the horizontal component of the force of the ground on the ladder leg at point A?
d) What is the vertical component of the force of the ground on the ladder leg at point E?

Homework Equations

Na is normal force at point A
Ne is normal force at point E
Fcy is the force at point C in the Y direction
Fcx is the force at point C in the X direction
L is the length of one side
l is the length of the tie

The Attempt at a Solution

I set up my equations like this:
1) Left side in the x: T-Fcx=0 same as on the right
2)Left side in the y: Na+Fcy-mg=0
3)Right side in the y: Ne-Fcy=0
4) Na-Ne-mg=0 (for the system)
5) torque about the point c: Fy*0+Fx*0-T*(L/2)*cos(theta)+Ne*l/2

to find theta i took the inverse sin of (.395/1.3)
so for torque i found .395Ne=1.24T
or T=.3189Ne

but when I tried to solve for my 5 unknowns I keep going in a never ending circle. I think once i find the Tension I can find parts b) c) and d)

 

[tvavanasd]

...
I set up my equations like this:
1) Left side in the x: T-Fcx=0 same as on the right
2)Left side in the y: Na+Fcy-mg=0
3)Right side in the y: Ne-Fcy=0
4) Na-Ne-mg=0 (for the system)
5) torque about the point c: Fy*0+Fx*0-T*(L/2)*cos(theta)+Ne*l/2
...
I think once i find the Tension I can find parts b) c) and d)

Have you kept your force direction assumptions consistent? A free body diagram would help if you haven't completed one. In equation 3, you assume that Ne is positive (up I assume, but in equation 4 it is negative (down). I haven't checked everything.

It isn't necessary to solve in order. From geometry, you can pretty easily determine parts b and d. Part c is rather trivial (I think).