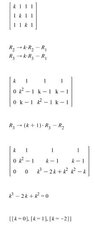Discussion Overview
The discussion revolves around determining the values of \( k \) for which a given system of equations has infinite solutions, no solutions, or a single solution. Participants explore the implications of the determinant of the system and the conditions under which different types of solutions arise, engaging in technical reasoning and analysis of their findings.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants propose that for \( k=0 \) and \( k=1 \), the system has infinite solutions, while for \( k=-2 \), there is no solution.
- One participant questions their earlier conclusion about \( k=0 \) leading to infinite solutions, noting that a computational tool (Maple) indicated a single solution instead.
- Another participant highlights that setting \( k^2+k-2=0 \) leads to a division by zero when \( k=0 \), which complicates the solution process.
- There is a discussion about the determinant of the system being zero, with some participants arguing that this condition does not necessarily imply no solutions but rather indicates either no solutions or infinitely many solutions.
- One participant presents a detailed calculation of the determinant and its implications, suggesting that the system has a solution for any \( k \neq -2 \), despite earlier claims about \( k=1 \) leading to a zero determinant.
- There is a call for clarification regarding the implications of row operations in Gaussian elimination, particularly when \( k=0 \) is involved.
Areas of Agreement / Disagreement
Participants express differing views on the implications of the determinant and the conditions under which solutions exist. There is no consensus on the correct interpretation of the results for specific values of \( k \), particularly regarding \( k=0 \) and \( k=1 \).
Contextual Notes
Participants note limitations in their reasoning, particularly regarding the handling of division by zero and the implications of Gaussian elimination. The discussion remains open-ended with unresolved mathematical steps and assumptions.