Why Is the Green Observer Always the Bent One in the Twin Paradox?

[SamRoss]

TL;DR

I read through "A Geometrical View of Time Dilation and the Twin Paradox" from the FAQ but I still have questions.

I feel a little guilty writing this post because I'm sure there are people here who are tired of answering questions about the twin paradox, hence the FAQ post on the subject, but there's something which is still nagging me. First I have a question about the FAQ post itself. Toward the bottom of the page, the equation

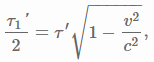is written. There was a similar equation,

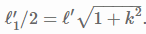, in the prelude at the top. I'm confused by the left side of these equations. My understanding of what was meant by $\tau^{'}_1$ and $l^{'}_1$ was that they were the lengths of the red line segments in the diagrams, so the effect of putting them over 2 would be to cut them in half. But this is precisely what was said to be an error. That is, $\tau^{'}_1/2$ and $l^{'}_1/2$ are not half the length of the line segments. Could someone straighten this out for me?

Okay, now for what's really nagging me. I feel like this really gets to the heart of why schmucks like me can't wrap our heads around the paradox (or maybe it's just me). Despite the confusion I described above, I think the FAQ post did a pretty good job of shedding light on the issue. We start with a set of perpendicular axes and calculate the proper times for the red (stays on Earth) observer and green (flies off and comes back) observer. We see that the proper time for the red guy is greater than the proper time for the green guy. Then we switch to oblique axes, we work through it again, and voila! The proper time of the red guy is still bigger. I know I should be satisfied by this but there's something that still troubles me and, like I said, I think it gets to the heart of what's so unsettling about the paradox. Why is the green guy always the bent one? Here's what the basic diagram looked like in the FAQ...

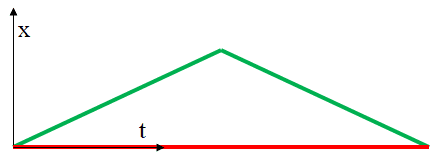Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...

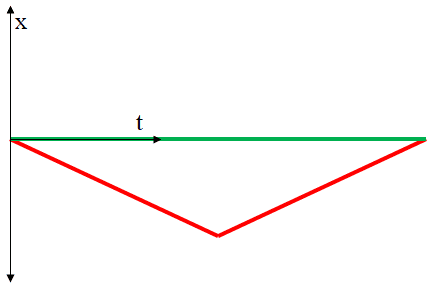
In this case, the green guy looks like he's staying put while the red guy moves first in the negative direction and then back. It seems like we should be able to go through all the same steps that were explained in the FAQ and discover that this time the green guy's proper time is the greater one whether we use perpendicular or oblique axes. Something tells me I can't be the only one who is thinking along these lines so if anyone can explain where the error in my reasoning is, you'd not only be helping me out but maybe others as well. Perhaps an explanation could be added to the FAQ.

 

[FactChecker]

The situation of the twins is not symmetric. Even without any external reference, the traveling twin knows that he is following an accelerated path when he reverses direction. The only unaccelerated paths in his reference frame is a straight line (geodesic) in his spacetime. When he deviates from that, he is accelerating. I think that a good video is Twin Paradox in General Relativity.

 

[Nugatory]

In this case, the green guy looks like he's staying put while the red guy moves first in the negative direction and then back. It seems like we should be able to go through all the same steps that were explained in the FAQ and discover that this time the green guy's proper time is the greater one whether we use perpendicular or oblique axes.

It does seem that way, and that’s why it’s called the twin paradox - you’ve just put your finger on the argument that makes it seem paradoxical. However, there is a resolution: the formula that says the proper time between two events is $\tau=\sqrt{\Delta{t}^2-\Delta{x}^2}$ is only correct if the x and t coordinates are those of an inertial frame. The frame in which the green line is straight is not inertial, so you can’t use that formula.

 

[pervect]

On a plane in space, which is Euclidean, the shortest distance between two points is a straight line. Any path other than a straight line will be a longer path. It doesn't matter what sort of diagram you draw, this is a physical fact about the geometry of the plane.

The geometry of space-time is less familiar. It goes by the name of "Lorentzian", but I don't think knowing the word explains much. The property it has though, is that the closest equivalent to a straight line is the worldline of an inertial observer.

The worldline of an observer who turns around is simply not inertial.

The analogy between the twin paradox and the straight line on the plane isn't quite perfect. Do to what's basically a sign difference, the path of an inertial observer in the geoemtry of special relativity has the longest elapsed time. Any other possible path that an observer could take will have a shorter elapsed time. This is a basic property of an inertial observer.

The obsever, or twin, who turns around simply isn't inertial, and that's why the argument can't be reversed.

 

[Dale]

Why is the green guy always the bent one?

In relativity the amount of bending of a worldline is measured by an accelerometer. If the accelerometer reads 0 then the worldline is straight (the technical term is “geodesic”). So the green guy’s line is bent because his accelerometer is the one that records a bend. The time of the accelerometer reading determines the time of the bend and the magnitude and direction of the reading determine the sharpness and direction of the bend.

The accelerometer readings are directly related to the previous posters discussions about inertial and non-inertial.

it really really feels like we ought to be able to draw a diagram like this

The accelerometer readings don’t support that drawing. In fact, they directly contradict it.

 

[SamRoss]

The situation of the twins is not symmetric. Even without any external reference, the traveling twin knows that he is following an accelerated path when he reverses direction. The only unaccelerated paths in his reference frame is a straight line (geodesic) in his spacetime. When he deviates from that, he is accelerating. I think that a good video is Twin Paradox in General Relativity.

I'm completely fine with this explanation. In fact, it's what I was leaning toward already. Acceleration and gravitational fields, implying general relativity, seem like the only plausible way to break the apparent symmetry of the situation. However, the FAQ post that I read here on PF, as well a book I am reading now, make it seem as though the problem can be solved merely by taking a closer look at the relativity of simultaneity. Are these explanations spurious or can the twin paradox actually be solved within the confines of SR without having to look to GR for the answer?

 

[Dale]

Acceleration is not exclusive to GR. You can handle acceleration just fine in SR. It is an oddly persistent myth that acceleration implies GR.

 

[FactChecker]

Are these explanations spurious or can the twin paradox actually be solved within the confines of SR without having to look to GR for the answer?

Experts (I am not one) tell me that SR completely handles the problem. If you look at the logic, there is little or nothing in GR that is necessary. Some of the GR references made it easier for me to understand and accept, but I think that SR would do just as well. Certainly, a direct application of the correct SR equations gives the desired result.

 

[Dale]

Some of the GR references made it easier for me to understand and accept, but I think that SR would do just as well.

Coordinates and tensors also make it easier. But GR does not “own” tensors. So even using tensors doesn’t mean you have left SR.

 

[SamRoss]

In relativity the amount of bending of a worldline is measured by an accelerometer. If the accelerometer reads 0 then the worldline is straight (the technical term is “geodesic”). So the green guy’s line is bent because his accelerometer is the one that records a bend.

Should I be thinking of an actual physical accelerometer that the green and red guys carry with them or just a mathematical device for measuring the curve of a worldline? If it is just a mathematical device, then that means we have chosen to draw the worldline as bent which again begs the question, "Why not draw the green one straight and the red one bent?" If we are thinking of an actual physical accelerometer then the only reason for it to record a non-zero acceleration would be due to the influence of other objects apart from the red and green guys themselves, wouldn't it? In that case, the resolution of the twin paradox would seem to require more than just an analysis of a bent line in a space-time diagram.

Also, I know that accelerations can be handled in SR but can the source of the accelerations be explained without reference to any other matter in the universe besides the red and green guys? Here's another way to put it: Create a universe with only the red guy and the green guy, both the same age. Some "proofs" that I've seen involve a third person so you can throw him in too if you like. Furthermore, you're allowed to start these guys off with any initial velocity and orientation relative to one another that you like. Can you create a situation where one person ends up an old man while the other remains a young hot shot?

 

[Dale]

Should I be thinking of an actual physical accelerometer

Yes.

If we are thinking of an actual physical accelerometer then the only reason for it to record a non-zero acceleration would be due to the influence of other objects apart from the red and green guys themselves, wouldn't it?

No. I am not sure why you think this. Can you explain your reasoning? Accelerometers do not need any external reference and their readings are not relative (the technical term is “frame invariant”)

 

[SamRoss]

You answered "no" to the accelerometer recording a non-zero acceleration due to any influence other than the red and green guys. So if the red and green guys - and their accelerometers - are the only objects in the universe, how could you get one of their accelerometers to be non-zero while the other is zero? I would understand a lot better if I knew the method for achieving this.

 

[Dale]

So if the red and green guys - and their accelerometers - are the only objects in the universe, how could you get one of their accelerometers to be non-zero while the other is zero?

For example one twin urinates forcefully in one direction to generate a “water rocket” while the other doesn’t.

It doesn’t matter how the twin accelerates. It is your scenario so you are free to specify any means you wish. Regardless of the mechanism of the acceleration the accelerometer records the effect on the worldline.

 

[Orodruin]

Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...

You are not thinking geometrically here. Trying to get you to think geometrically was the entire reason of first introducing the equivalent statements in a regular Euclidean plane where Pythagoras' theorem holds. The underlying geometrical object is the triangle, so draw a triangle like the one in the Insight (put no axes). Now hold the paper in front of you and call the horizontal direction x and the vertical y. Your geometrical object is the paper, clearly it does not matter how you orient the paper. Regardless of how you turn it, the sides of the triangle are going to have the same lengths and the angles between the sides also remain the same.

The point is that, although spacetime geometry works differently and rotations are replaced by Lorentz transformations, the same ideas still hold. Regardless of how you Lorentz transform the triangle, you cannot change the proper time of the world-lines, nor can you change which world-lines are curved.

My understanding of what was meant by τ′1τ1′\tau^{'}_1 and l′1l1′l^{'}_1 was that they were the lengths of the red line segments in the diagrams, so the effect of putting them over 2 would be to cut them in half. But this is precisely what was said to be an error.

No. It is perfectly fine to do that as long as you make sure that you are actually getting half the proper time or length, which you have to base upon which coordinate system you are using. When computing $\tau_1'$, I am using the coordinate system where the half-journey occurs at the same coordinate time for both observers.

 

[FactChecker]

If one wanted to propose that acceleration is relative, then he would have to model the effect of the entire Universe accelerating while the (prior) traveling twin is assumed to be stationary. The result should be identical. That would certainly require GR to exert the forces on the stationary twin caused by the accelerating universe.

A similar effort regarding the force of a counter-rotating universe was looked at in The Machian Origin of the Centrifugal Force. I am not qualified to evaluate that work.

 

[SamRoss]

For example one twin urinates forcefully in one direction to generate a “water rocket” while the other doesn’t.

It doesn’t matter how the twin accelerates. It is your scenario so you are free to specify any means you wish. Regardless of the mechanism of the acceleration the accelerometer records the effect on the worldline.

I like that answer. It confirms what I've been suspecting. In all the explanations of the twin paradox, there's usually no mention of any physical distinction between the two guys. It's implied that you can reason your way out of the paradox just by looking at the geometry - at the curves or the accelerations or the use of multiple frames to describe one observer. The break in the symmetry is in the diagram. Well, I'm becoming more and more convinced that it's not. The break in the symmetry can only be found in the physical means through which the acceleration is achieved, whether that's firing rockets or urinating or whatever. One guy does it and the other guy doesn't and that's the real source of the age difference.

 

[Orodruin]

The break in the symmetry can only be found in the physical means through which the acceleration is achieved, whether that's firing rockets or urinating or whatever.

This is incorrect. You can reason through pure geometry, but you need to understand the geometry used.

Do you understand that the lengths and angles in the triangle you draw on a piece of paper do not change regardless of how you rotate the paper?

 

[PeroK]

I like that answer. It confirms what I've been suspecting. In all the explanations of the twin paradox, there's usually no mention of any physical distinction between the two guys. It's implied that you can reason your way out of the paradox just by looking at the geometry - at the curves or the accelerations or the use of multiple frames to describe one observer. The break in the symmetry is in the diagram. Well, I'm becoming more and more convinced that it's not. The break in the symmetry can only be found in the physical means through which the acceleration is achieved, whether that's firing rockets or urinating or whatever. One guy does it and the other guy doesn't and that's the real source of the age difference.

Well, actually, my favourite version of the paradox has no acceleration at all. It's described here:

https://en.wikipedia.org/wiki/Twin_paradox#Role_of_acceleration
In addition, one fundamental problem with using acceleration as the physical mechanism is when you compare the following. Let's call the twins A and B.

a) A & B start together; B accelerates away, eventually slows down, accelerates in the opposite direction, slows down and arrives home. That's four physical acceleration phases.

b) B starts with the traveling velocity. As B passes A they synchronise their clocks, B travels, slows down, accelerates in the opposite direction and as B passes A they compare their clocks without B slowing down. That's only two acceleration phases.

c) Whenever B is accelerating, A accelerates too, but backwards and forwards so that A never goes very fast or travels far from the starting point. In this case, the total periods of acceleration for both A and B can be made the same. Yet there is still differential ageing of B.

 

[Orodruin]

In addition, one fundamental problem with using acceleration as the physical mechanism is when you compare the following.

The fundamental problem with using acceleration is that proper time is based on lengths, not on curvature, of the world-line. The entire point behind differential ageing is that a straight line in Minkowski spacetime is a global minimum for the proper time. Once you have that down you can start talking about the physical observables of not being on a straight line and so on.

 

[PeroK]

The fundamental problem with using acceleration is that proper time is based on lengths, not on curvature, of the world-line. The entire point behind differential ageing is that a straight line in Minkowski spacetime is a global minimum for the proper time. Once you have that down you can start talking about the physical observables of not being on a straight line and so on.

I was challenging the OP's conclusion that a period of acceleration might act physically as an anti-ageing potion!

 

[A.T.]

Why is the green guy always the bent one? Here's what the basic diagram looked like in the FAQ...

Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...

If you want to see the age difference directly, you can use a space-propertime diagram. Here the length of each path represent the coordinate time t, so both paths have the same length, but they end up at different proper times (age differently). You also have to account for the acceleration of the travelers frame, which is simplest assuming constant acceleration, which results in curvlinear coordinates:

Here is a comparison of Minkowski and Epstein diagrams for the 3 inertial frames of the twins (traveler has constant speed with instantaneous turn around): http://www.adamtoons.de/physics/twins.html

 

[Ibix]

Now I know I must be wrong somewhere, but it really really feels like we ought to be able to draw a diagram like this...

In this case, the green guy looks like he's staying put while the red guy moves first in the negative direction and then back.

You can try doing that, but the relativity of simultaneity bites you. Here are three Minkowski diagrams showing the same scenario. I've used your colour convention, and the only thing I've done is add a red cross marking a party the red guy holds at the midpoint of the experiment. The first diagram is in the frame where the red guy is at rest:

The next is in the frame where the green guy is at rest on the outbound leg:

The final one is in the frame where the green guy is at rest on the inbound leg:

Now let's try to construct your diagram, by snipping the top off the second diagram and the bottom off the third diagram, keeping only the parts where the green guy is at rest in each frame. That looks like this:

That's pretty much what you drew (I've done a literal cut-and-paste, which is why bits of axes appear) - but where has the red guy's party gone? The problem is that in the outbound frame it happens after turnover, and in the inbound frame it happens before turnover. The two frames have different ideas of what "at the same time as turnover" means (this is the relativity of simultaneity), and the party gets lost in the cracks. So that means that this diagram is not an accurate representation of reality.

You can, of course, construct a more complicated diagram that shows the green guy as "at rest", but the red guy's path does not look like you have drawn it. Figure 9 in https://arxiv.org/abs/gr-qc/0104077 shows one way of doing it - the dashed red line ("Alex") corresponds to our red guy and the solid red line ("Barbara") to the green guy.

 

[Dale]

one fundamental problem with using acceleration as the physical mechanism

There is no problem with using acceleration as the physical mechanism for the specific question asked. The OP specifically asked why one twin’s line was always drawn as bent. The specific question was about the bend and the accelerometer clearly addresses that.

The fundamental problem with using acceleration is that proper time is based on lengths, not on curvature

Yes, but again, the acceleration does answer the specific question of the bend.

 

[Dale]

The break in the symmetry can only be found in the physical means through which the acceleration is achieved, whether that's firing rockets or urinating or whatever. One guy does it and the other guy doesn't and that's the real source of the age difference.

Please be careful in your reasoning here. I discussed the link between the acceleration and the bend in the worldline. The age difference is determined by the length of the worldline, not the bend. The two are related, but not the same.

For example, in Euclidean geometry the sum of the length of two sides of a triangle is greater than the length of the third side. The path formed by the two sides of the triangle have a bend in it. The bend is definitely related to the fact that the lengths are different, because the bend indicates which path is straight and a straight line is the shortest path between two points. But you would not say that the bend in the triangle is the source of the extra length.

The source of the length is the entire path. Different paths simply have different lengths, and the straight path has the shortest length. The straight path is the one that does not bend.

Similarly for the twins, the proper time is the length of the path and the proper acceleration is the bend. Different paths through spacetime simply have different lengths, with the geodesic being the longest path. The geodesic is the one that does not bend as determined by the accelerometer.

Again, the bend in the spacetime path is identified by the accelerometer but the clock difference is identified by the length of the spacetime path. They are related, but not the same.

 

[FactChecker]

Mathematically, the acceleration and velocity of an object-centered coordinate system can only be defined relative to another object. No derivatives can be defined otherwise. Purely mathematically, all motion and its derivatives are relative. In an object-centered coordinate system, the object at the center never moves at all. But that is not the situation being addressed in SR and GR. There are physical effects that can identify which coordinate systems are accelerating and which are inertial. Since SR and GR are theories about physical behavior, it is legitimate to use physical effects to identify inertial coordinate systems.

 

[SamRoss]

This is incorrect. You can reason through pure geometry, but you need to understand the geometry used.

Do you understand that the lengths and angles in the triangle you draw on a piece of paper do not change regardless of how you rotate the paper?

I understand that perfectly well. Do you understand that if I give you a blank piece of paper then you have the freedom to choose which lines will be bent and which won't? If I say, "Make part of the triangle red and part of it green," then without any further guidance you would be just as entitled to make either the red line or the green line bent? That is why I think the FAQ post is unsatisfactory; not inaccurate, just incomplete. It begins after the green line has already been bent and does not say why.

I may not be an expert, but I think I'm right in saying that the worlldline of an object in Minkowski space will be a straight line unless that object is subject to a potential. It is that potential, caused by the physical distinctions between the two observers (i.e. firing a rocket) that is the reason only one of the worldlines in Minkowski space is bent. Once that has been established, I agree with you that the rest is geometry and both observers will agree that the red guy's proper time is greater regardless of which coordinate system is used. Omission of the original cause of the bent worldline is the source of the confusion in the twin paradox, not the math that follows it.

 

[Orodruin]

Do you understand that if I give you a blank piece of paper then you have the freedom to choose which lines will be bent and which won't?

Either the line you draw is straight or it is not. The lines do not exist before you draw them because that defines what the lines are.

If I say, "Make part of the triangle red and part of it green," then without any further guidance you would be just as entitled to make either the red line or the green line bent?

This is not correct. If you want to describe a line that bends and a line that is straight, the straight line is going to be straight and the bent line will be bent. There is no getting away from that. What color you chose is obviously irrelevant. The physical thing is whether the line is bent or not.

I may not be an expert, but I think I'm right in saying that the worlldline of an object in Minkowski space will be a straight line unless that object is subject to a potential. It is that potential, caused by the physical distinctions between the two observers (i.e. firing a rocket) that is the reason only one of the worldlines in Minkowski space is bent. Once that has been established, I agree with you that the rest is geometry and both observers will agree that the red guy's proper time is greater regardless of which coordinate system is used. Omission of the original cause of the bent worldline is the source of the confusion in the twin paradox, not the math that follows it.

It is irrelevant why the object accelerates. The only relevant thing is the geometry. In curved spaces you can have straight lines between the same points that have different lengths. How the worldlines get their shape is also irrelevant, the only important thing is that they have that worldline.

 

[FactChecker]

Consider the object-centered coordinate system of each twin. Neither twin moves at all in its respective object-centered coordinate system other than through time. Their intrinsic mathematical properties are identical. The only way to identify one as accelerating and the other as inertial is to use physical effects (eg felt acceleration) or references to other objects (eg. the universe).

But that is OK. Both SR and GR are all about the physics so using physical effects to identify an accelerating reference frame is, IMHO, legitimate.

 

[SamRoss]

If you want to see the age difference directly, you can use a space-propertime diagram. Here the length of each path represent the coordinate time t, so both paths have the same length, but they end up at different proper times (age differently). You also have to account for the acceleration of the travelers frame, which is simplest assuming constant acceleration, which results in curvlinear coordinates:

View attachment 245072

Here is a comparison of Minkowski and Epstein diagrams for the 3 inertial frames of the twins (traveler has constant speed with instantaneous turn around): http://www.adamtoons.de/physics/twins.html

The Epstein diagram is interesting. Respectfully, however, I do not think it answers my question. As I just said to Orodruin, an object will follow a straight line in Minkowski space (and I assume in Epstein space as well) unless subject to a potential. Omitting the influence of the potential on the trajectory means you will not be able to explain why one worldline is bent (or curved) and the other is straight in the first place.

 

[Orodruin]

The Epstein diagram is interesting. Respectfully, however, I do not think it answers my question. As I just said to Orodruin, an object will follow a straight line in Minkowski space (and I assume in Epstein space as well) unless subject to a potential. Omitting the influence of the potential on the trajectory means you will not be able to explain why one worldline is bent (or curved) and the other is straight in the first place.

Again, it is completely irrelevant why the worldline is curved. It is not even important that it is curved (apart from the fact that it needs to get to the same point as the other worldline - which in Minkowski space requires bending) - it is perfectly possible to create a situation in GR where inertial observers experience differential ageing. It is also not clear what you mean by "subject to a potential" in this context. There is no need for the accelerating force to be conservative.