Tangeton
- 62
- 0
(b) (i) A satellite of mass 2520 kg is at a height of 1.39 × 107m above the surface of the Earth. Calculate the gravitational force of the Earth attracting the satellite. Give your answer to an appropriate number of significant figures.
Worked out to be F = 2.45 x 103
The satellite in part (b)(i) is in a circular polar orbit. Show that the satellite would travel around the Earth three times every 24 hours.
The answer is F = (mv2)/R+h where F = 2.45 x103 to find the speed first.
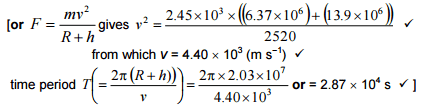
But no matter how I put that equation into the calculator, whether I use the valued stored in the calculator or type in exactly what it says, it is not 4.40 for speed but 4.439... so 4.44. Why is that?
This is a past exam question.
Worked out to be F = 2.45 x 103
The satellite in part (b)(i) is in a circular polar orbit. Show that the satellite would travel around the Earth three times every 24 hours.
The answer is F = (mv2)/R+h where F = 2.45 x103 to find the speed first.
But no matter how I put that equation into the calculator, whether I use the valued stored in the calculator or type in exactly what it says, it is not 4.40 for speed but 4.439... so 4.44. Why is that?
This is a past exam question.