How Can Integral Calculus Help Solve This Sphere and Cone Volume Problem?

[th0rbahn]

Here is an assigned problem:
http://www.stfx.ca/academic/mathcs/courses/calculus/Current_Projects/PROJECT%20I%20Spring%202007.doc

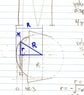
As it is a problem for my integral calculus class, I assume some integral calculus would be required to solve it, possibly dealing with the rate of change of the sphere as it descends down into the cone, but I'm not sure.

I'm not exactly looking for a complete solution, more of a thought process that would lead me in the right direction. Any help or thoughts on this is appreciated.

Thanks.

 

[AKG]

Case 1: the whole ball goes in.
If the ball has radius R, it displaces a volume of water of $\frac{4}{3}\pi R^3$.

Case 2: the whole ball doesn't go in, but at least half does.
Let R be the radius of the ball. Part of the ball sticks out above the opening of the cone. Say the part that sticks out above has volume v. Then the amount of water displaced is $\frac{4}{3}\pi R^3 - v$. You need to find an expression for v in terms of R, h, and r, where h and r are the height and radius of the cone, respectively.

Case 3: less than half the ball goes in.
The idea is the same as case 2, but the expression for v will be different.

 

[th0rbahn]

Thank you, that's quite helpful. Will the expression for 'v' in case 2 require an integral? Also, once we have an expression for water displaced in terms of the geometries of the cone and sphere, what technique would be used to find the radius which maximizes the volume of water? Would that be using optimization techniques from differential calculus?

 

[AKG]

Thank you, that's quite helpful. Will the expression for 'v' in case 2 require an integral?

Using integrals will be a good approach.

Also, once we have an expression for water displaced in terms of the geometries of the cone and sphere, what technique would be used to find the radius which maximizes the volume of water? Would that be using optimization techniques from differential calculus?

Yes.

 

[th0rbahn]

Hi again, I've worked through a lot of this but haven't quite been able to reach an answer yet.

The problem is when I reach the following integral:

http://thorbahn.net/misc/cone_integral.jpg

can such a thing be done to solve for volume only in terms of R, the radius of the sphere? That integral equal to v, the volume of the region of the sphere above the cone when the sphere is more than half "submerged".

Here is a scan of my work to reach this point:
http://thorbahn.net/misc/cone_problem.jpg

I commend anyone who takes the time to look at this for me.
Thanks.

 

[Werg22]

AKG, it is impossible for a ball to get half way in. Case 2 doesn't exist. For case 3, we have to note that the surface of the cone will be tangential to the ball. I'm thinking about the problem, but I can't find the condition for which a ball is either in case 1 or 3... thinking...

 

[th0rbahn]

I believe I have solved it since my last post, the work on the scanned page was correct and a more meticulous method for finding the integral made it solvable. For what it's worth, the radius which maximized the amount of water displaced was a value just a bit less than 1, yielding a displaced volume of 7.49. Half submerged resulted in 6.28 while completely submered was 5.30.

 

[Werg22]

You would have to show that because I'm convinced that it is impossible for a sphere to be half submerged.

Edit: sorry to be blunt, but I believe your work is wrong all around. Let me give you a pointer:

Find a function of the radius of the sphere vs the its width when its derivative is parallel to the a segment of the cone. To do this, simply illustrate the problem with a line (and its slope) and a circle. Let's call this width threshold width. If the threshold width is smaller than diameter of the cone, then, the cone will be tangential to the sphere. If the threshold width is larger than the diameter of the cone, then the ball gets "stuck". This means you need two functions for the displaced volume. Finally find the respective maxima and compare them.

 

[AKG]

It's impossible for at least half the ball to be submerged? You think a pea wouldn't fit in an ice cream cone?

 

[Werg22]

It's impossible for at least half the ball to be submerged? You think a pea wouldn't fit in an ice cream cone?

No, not at all. It's impossible for exactly half of it to be submerged. See my proposed solution, it doesn't exclude all or most of the sphere being submerged.

Edit: ok rereading case 2, I realize that you meant "more than half". A misunderstanding. Sorry.

 

[Werg22]

Okay. It is possible for exactly half of the ball to be submerged, I wasn't thinking right. What needs to be remembered is that the fact that the cone will be tangential to the ball.

 

[AKG]

If the cone is tangential to the ball and the ball is exactly half way in, then the vertex of the cone goes to infinity.

 

[Werg22]

Yes, that is if the cone is tangential to the ball at the radius. Funny, because this is why I kept on saying it's impossible for exactly half the ball to go in. However, it is possible - in the case the cone is tangential to the ball at some z, and then the lateral section of the cone extents the level of the radius of the ball.

 

[AKG]

Hi again, I've worked through a lot of this but haven't quite been able to reach an answer yet.

The problem is when I reach the following integral:

http://thorbahn.net/misc/cone_integral.jpg

can such a thing be done to solve for volume only in terms of R, the radius of the sphere? That integral equal to v, the volume of the region of the sphere above the cone when the sphere is more than half "submerged".

Here is a scan of my work to reach this point:
http://thorbahn.net/misc/cone_problem.jpg

I commend anyone who takes the time to look at this for me.
Thanks.

You calculated r wrong. I've attached something, it should help you figure out how to calculate r.

EDIT: actually, as Werg22 points out below, you're assuming the ball touches the cone at it's half-way point. This is wrong.

 

[Werg22]

AKG, do you agree that there is a problem with his method? The ball does not get stuck at it's radius, like he assumed.

 

[AKG]

Yes, I agree.

 

[th0rbahn]

hm. now I'm in a pickle because this is due tomorrow and for the last while I thought I was finished. any comments you have to add to your previous ones to help work through this would be appreciated, because right now it's not coming together.

 

[Werg22]

Hummm PM me.

 

[JasonRox]

It's impossible for at least half the ball to be submerged? You think a pea wouldn't fit in an ice cream cone?

Man, I laughed out loud. :rofl:

 

[th0rbahn]

No more assistance needed -- it has been solved. Maybe even correctly, too.

 

[nog]

how did you end up getting it? what was wrong with your origonal work?

 

[Werg22]

Oh okay then. Nog, check out your PM.

 

[AKG]

I'm sorry, I think I mislead you a little with the cases I drew up for you. You should only consider one case: the case where the ball is tangent to the cone and the ball isn't submerged below the opening of the cone. There's a part of your question that asks to explain why a ball that's too big or too small won't do it. The idea is that if the ball is submerged below the opening of the cone, it's too small, and if the ball is not tangent to the cone, it's too big, hence the case I just mentioned really is the only relevant case. In this case, there is a single formula for the volume submerged in terms of the radius R of the sphere. You find this formula using some trigonometric ratios and maybe some facts about similar triangles, then using integrals to express the volume. This will give you volume V(R) as a function of R. R is at its minimum r when the ball is just fully submerged. R is at its maximum r' when the point where the ball and the cone are tangent is on the rim of the cone. Find V(r) and V(r'). Find r'' between r and r' such that dV(r'')/dR = 0, and compute V(r''). The biggest of V(r), V(r') and V(r'') is what you want. Note this problem gets messy. There are tricks to keep it a little neat, but in the end I think it's bound to have some messy expressions with fractions and square roots and squares, etc. Good luck.

 

[th0rbahn]

that sounds more or less like what I ended up doing. Here is an image I drew up for this case:

http://thorbahn.net/misc/appendix[/URL] 3.jpg[/PLAIN] Thanks for the help for the past little while, I appreciate it.