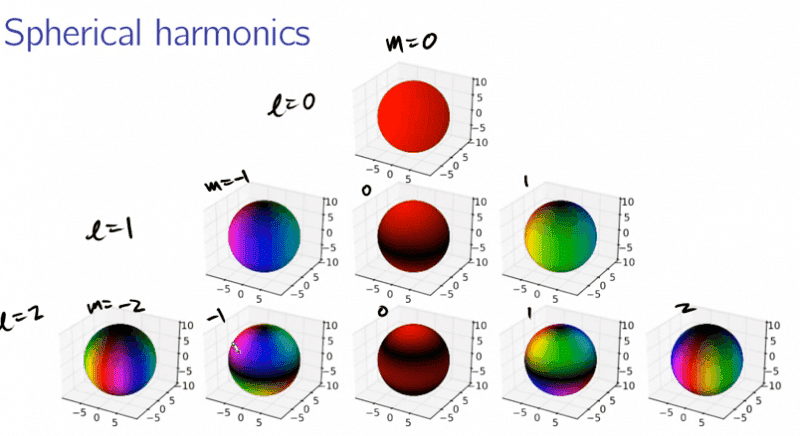
Not sure what the application is for your example, but the surface of a sphere may have modes of oscillation (radial surface motions).
Simplest way is for the entire surface to move in and out (the whole sphere gets smaller and bigger) - looks like l=0 m=0
Another way is for one half to move in as the other half moves out and vice versa - looks like l=1 m=0
Those are the only ones that look clear in the picture, to me; but the l and m numbers are continuing to identify the modes.
From there the sphere may be sectioned into four longitudinal quadrants where the opposing pairs make opposing motions.
Same for eight sections, four in one half and four in the other, etc...
And others where the moving parts are like the latitudinal bands around the Earth - looks like l=2 m=0
The sections and bands get complicated because they interact to form whole number counts, some required to be even numbers to support a repeating series of opposite polarities of motion (the longitudinal "slices"), and others not held to that constraint (the bands) because they don't repeat, they occupy the poles... the use of the m and l numbers are used to describe all combination possibilities completely.
Typically, colors may be used to distinguish which parts are moving in a direction at a moment to mark the polarities of the regions, and boundaries (node lines of no movement) between them.
These harmonic "motions" may in your example be analogous to some other oscillatory property that may not be a strict motion but rather a change in some other attributes like field strength, density, polarity, probability, etc...