How Does Adding a Damper Affect the Stiffness of Springs in Parallel?

AI Thread Summary
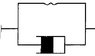
Adding a damper in parallel with springs affects the overall stiffness by modifying the total impedance, which is represented as k + sc in the Laplace domain. The springs in parallel combine their stiffness according to the formula 1/k(total) = 1/k1 + 1/k2, while the damper introduces a viscous element that influences the system's response. The interaction between the spring constants and the damping coefficient alters the dynamic behavior of the system. Understanding this relationship is crucial for analyzing damped harmonic oscillators. The discussion highlights the importance of considering both spring and damper characteristics in system design.
VooDoo
Messages
58
Reaction score
0
Hey guys,

I was just wanting to know, if there is a special way to add a damper in spring in parallel (as per the image below).

i know that springs in parallel is; 1/k(total) = 1/k1 + 1/k2...
 

Attachments

  • system.jpg
    system.jpg
    4 KB · Views: 688
Physics news on Phys.org
Put the spring in a viscous medium.
Actually any real spring is a little bit like that.
 
spring coeff: k
damper coeff: c

total impedance is k + sc

in laplace domain
 

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

Spring force after fixating with limited stiffness
Replies
9
Views
1K
Spring damper system without a mass
Replies
8
Views
9K
I Work-Energy Theorem for Moving Block and Spring System?
Replies
4
Views
2K
I Calculating Viscous Damper Energy in Spring-Mass Systems
Replies
15
Views
7K
How to solve spring mass damper system manually?
Replies
16
Views
3K
How Do You Calculate the Natural Angular Frequency of a Dual-Spring System?
Replies
5
Views
3K
Engineering Control System mass spring damper
Replies
0
Views
1K
In dynamics, do we assume springs always resist motion?
Replies
9
Views
2K
Determining energy from spring arrangements (parallel&series)
Replies
2
Views
3K
External damping force in Mass Spring Damper system
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top