shyta
- 56
- 0
Homework Statement
This was a concept question my lecturer gave us, and although he tried to explain it thoroughly, I still didn't get it. So I was hoping someone could help me out.
There are 2 parts to this question
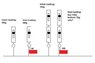
Firstly a spring balance is attached hanging from a celling using a string. The spring balance is then lightly pulled till it reads 100g. This end of the spring balance is then tied to the floor using a string.
The first question goes as what would happen if a 50g mass is hung on the the end of the spring balance.
The 2nd question goes as what would happen if there are now 2 spring balances in series and a 100g mass is hung on the end.
The Attempt at a Solution
I understand how to do the first question, as the mass is hung the tension in the string which is attached to the floor is reduced. Sort of like a compromising way, thus the reading still remains as 100g.
However, I didn't get the second part. The answer was that the higher spring balance would read 125 and the one below 75g. Can someone explain this to me please?