Spring constant matrix and normal modes (4 springs and 3 masses)

[LCSphysicist]

Homework Statement

ALl below

Relevant Equations

ALl below

We need to find the normal modes of this system:

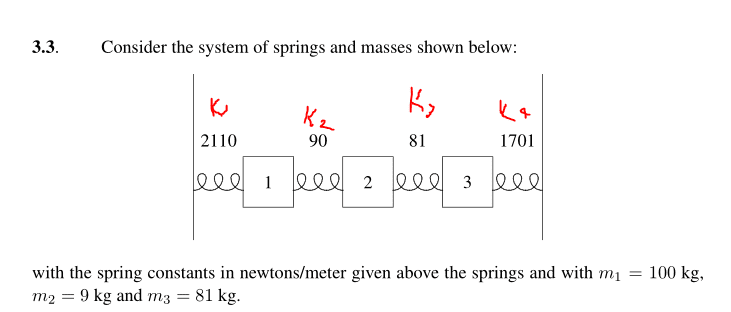
Well, this system is a little easy to deal when we put it in a system and solve the system... That's not what i want to do, i want to try my direct matrix methods.

We have springs with stiffness k1,k2,k3,k4 respectively, and block mass m1, m2, m3
And we need to annul the determinant of

, not just, i supposed the displacement Z as complex, so we need real angular frequencies.

To mount the matrix K, we need to know all Kij, being Kij the spring stiffness equivalent if we move just block j and analyze the motion of block i, j can be equal i.

So making all the things, we end with:

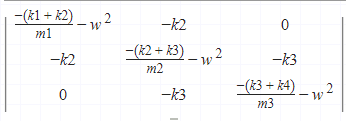
Apparently this is wrong, i found just complex w, what is the problem?

 

[haruspex]

Try the same method on a much simpler arrangement, one you can easily check from first principles. Note where the signs disagree.

 

[LCSphysicist]

Try the same method on a much simpler arrangement, one you can easily check from first principles. Note where the signs disagree.

Yeh that's enough... thank