Stability of Drink and Bottle on Train Table

[TFM]

Homework Statement

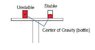
You are riding in a train and have just opened a bottle of beer. Prove that for your bottle to be as stable as possible on the table (which is shaking), you should drink sufficient beer such that the surface of the beer coincides with the centre of gravity of the partially filled bottle. You may wish to begin by assuming that the bottle is of constant cross-section.

The condition above for maximum stability is actually independent of the shape of the bottle. Give a logical argument for why this is the case.

Homework Equations

The Attempt at a Solution

I am not quite sure. I would have thought that to be the most stable the centre of gravity for the drink and the bottle should be in the same place - it appears I am mistaken. Any ideas?

 

[Perillux]

My reasoning is that if the top of the beer is below the bottles center of mass then that configuration will allow the maximum amount of mass(liquid) below the bottles center of mass, and no mass(liquid) above the bottles center of mass.
Because the bottle has less mass above it's center of mass, it will be less prone to tipping over, and all the mass below that point will help to stabilize it.

 

[TFM]

So, with the attached Diagram

A, which has a level over the Centre of Gravity, has more mass to weigh it down, but it is above the centre of gravity so the sloshing as it moves about has more effect and can push it over.

C, which has a level under the Centre of Gravity, has less to slosh around, and is under the centre of mass, meaning it will provide less effect to pushing the bottle, but the mass is significant decreased so has less pushing it onto the table

B, which has the level at the centre of Gravity, has a balance between the mass to keep it down, against the amount of liquid sloshing around to tip the bottle over.

Does this make sense? How would you prove it? I am assuming some formulas will be required?

TFM

 

[TFM]

Any ideas how to actually prove it?

TFM

 

[TFM]

Are there any formulas that could be useful for this problem?

TFM

 

[dotty123]

Remember that the centre of mass will get lower as you drink more beer.

 

[Perillux]

I'm not so sure about that dotty123. The problem is talking about the center of mass of the bottle, not the bottle+luquid. At least that is what I'm thinking.

TFM: If I am correct, then I would guess that B is the most stable. Because it has more mass than C to hold it down, but none of that mass is above the bottles center of mass, like in A.

 

[dotty123]

Isn't it asking about the centre of mass of the partially filled bottle? not just the bottle. Surely, if you're trying to calculate the stabililty of a drink, you have to take into account the mass of drink itself?
The drink will be most stable when the entire centre of mass is lowest. This can be calculated by combining the centre of mass of the bottle and the centre of mass of the liquid. Then you just need to find where it is at a minimum.