Anchovy
- 99
- 2
When reading about GUTs you often come across the 'Standard Model decomposition' of the representations of a given gauge group. ie. you get the Standard Model gauge quantum numbers arranged between some brackets. For example, here are a few SM decompositions of the SU(5) representations \textbf{5}, \textbf{10}, \textbf{15} and \textbf{24}.
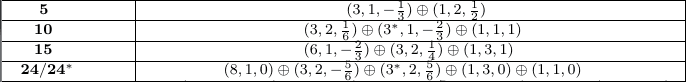
So, for instance this is telling us that the representation \textbf{5} will contain fields that are either
(SU(3)_{C} triplet, SU(2)_{L} singlet, hypercharge \tfrac{1}{2}Y = -\tfrac{1}{3}) for the (3, 1, -\tfrac{1}{3}),
or
(SU(3)_{C} singlet, SU(2)_{L} doublet, hypercharge \tfrac{1}{2}Y = \tfrac{1}{2}) for the (1, 2, \tfrac{1}{2}).
That's straightforward enough. However, I can't seem to find anything online explaining how these have been determined. I can find plenty about how you might go about constructing the \textbf{10}, \textbf{15} and \textbf{24} starting from combinations of the fundamental \textbf{5} by the 'Young's Tableaux' method, but nothing about starting with one of these SU(5) representations and breaking them down. Can anyone explain or link to an explanation?
So, for instance this is telling us that the representation \textbf{5} will contain fields that are either
(SU(3)_{C} triplet, SU(2)_{L} singlet, hypercharge \tfrac{1}{2}Y = -\tfrac{1}{3}) for the (3, 1, -\tfrac{1}{3}),
or
(SU(3)_{C} singlet, SU(2)_{L} doublet, hypercharge \tfrac{1}{2}Y = \tfrac{1}{2}) for the (1, 2, \tfrac{1}{2}).
That's straightforward enough. However, I can't seem to find anything online explaining how these have been determined. I can find plenty about how you might go about constructing the \textbf{10}, \textbf{15} and \textbf{24} starting from combinations of the fundamental \textbf{5} by the 'Young's Tableaux' method, but nothing about starting with one of these SU(5) representations and breaking them down. Can anyone explain or link to an explanation?