PhanthomJay said:
looks good error here...BZ = f*(tan h) You are correct that Na and Nb cannot be equal here, from your sum of moments equation. There is yes indeterminancy in the friction force calculations for Fa and Fb, but the usual assumption is that they are equal, on the basis that the brakes are applied on each wheel similtaneously. I suppose that if you had brakes applied on one wheel only, say A, then Fb would be zero, or if you applied the brakes on A first, the bike stops, then you apply the brakes on B, Fb would still be zero, but there is no way to determine this, so assume Fa=Fb. Your work looks very good other than the trig error.
haruspex said:
I'm not so sure. If that is the case then the crossbar would be under tension. I think an argument can be made that typically the frictional forces would be in proportion to the normal forces. Certainly that will be the case when the limit of static friction is reached.
PhanthomJay said:
looks good error here...BZ = f*(tan h) You are correct that Na and Nb cannot be equal here, from your sum of moments equation. There is yes indeterminancy in the friction force calculations for Fa and Fb, but the usual assumption is that they are equal, on the basis that the brakes are applied on each wheel similtaneously. I suppose that if you had brakes applied on one wheel only, say A, then Fb would be zero, or if you applied the brakes on A first, the bike stops, then you apply the brakes on B, Fb would still be zero, but there is no way to determine this, so assume Fa=Fb. Your work looks very good other than the trig error.
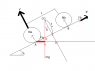
Ups yes I made that mistake. I have recalculated everything using these four equations:
1. fa=fb
2. Sum Ma= -mg*(cos(h)*(L/2- f*tg(h))) + Nb*L = 0
3. Sum Fx= Fa + Fb -mg sin(h)=0
4. Sum Fy= Na + Nb -mg cos(h)=0
From the third equation is easy to obtaing fa and fb:
fa=fb=mg sin(h)/2
Using the fourth equation I get:
Nb= mgcos(h) - Na
And I use that on the second equation so:
-mg*cos(h)*(L/2- f*tg(h))) + (mgcos(h) - Na )*L = 0
Na= mg cos(h) (1- (L/2 -f * tng(h))/L )
Using this value now I can calculate Nb:
Nb=-mg cos(h)/L * (L/2 -f*tg(h))
Using f=1 meter ; Mass= 115 kg; h=45º ; L=1meter I get these results:
Na=1195,5 N (121 kg)
Nb= 398,5 N (40 kg)
These results look like quite surprising to me because only at 45º you have three times more weight at the rear than at the front.
haruspex said:
I'm not so sure. If that is the case then the crossbar would be under tension. I think an argument can be made that typically the frictional forces would be in proportion to the normal forces. Certainly that will be the case when the limit of static friction is reached.
I tried to use your assumptions, so I had these four equations:
1. Nb*Fa=Fb*Na
2. Sum Fx= Fa + Fb -mg sin(h)=0
3. Sum Fy= Na + Nb -mg cos(h)=0
4. Sum Ma= -mg*(cos(h)*(L/2- f*tg(h))) + Nb*L = 0 = A+ Nb*L
I´ll try to show how I calculated the unknown quantities, using the second equation I have fa as function of fb:
fa= mg sin(h) – fb , relation 1
From the first equation:
Nb=Na * fb/fa
From the fourth equation, where I defined A to write less:
A + Na * fb * L / fa = 0 ----> Na= -A * fa/fb * L
Substituting on the third equation:
-A*fa/fb*L - A*fa*fb/fb*fa*L= mgcos (h), I cancel fa fb on the second term and I get fa as function of fb:
fa= (-1-Lmg cos(h)/A)*fb , relation 2
Using relations 1 and 2:
mg sin(h) – fb = ( -1 -Lmg cos(h)/A)*fb
fb( 1-( 1+ L mg cos(h))/A)= mg sin(h)
Now I use the value of A and this equations leads to:
fb= tg(h)/L * ( -mg cos(h) * (L/2 – f*tg(h))) , but tg(h)= sin (h) / cos (h) so:
fb=-mg sin(h) (½ – f*tg(h)/L)
To calculate fa I use relation 1 but knowing the value of fb so :
fa= mg sin(h) + (mg sin(h)/L *( L/2 -f tg(h))= mg sin(h) (3/2 – f tg(h) / L)
Using the fact that Na= -A fa/ fb L , I obtain:
Na=(mg cos(h) (L/2 – f tg(h))/L)* (-1 * (3/2 – f tg(h)/L)/(1/2 -f tg (h)/L))
Nb= mgcos(h) +Na
With the same values as before f=1m, h=45º, L=1m, I get these answers for Na and Nb:
Na= (115* 9,81*cos(45) (0,5 -1*1))/1 *(-1 *(3/2-1)/(1/2 -1))= -398,86 N
Nb= 115*9,81*cos(45)-398,86= 398,86 N
I think these results are a complete nonsense because the minus sign at Na it´s absurd, and the modulus should not be the same Na should be much bigger.
I´ll have a look at the mess of the calculations and if I see the mistake I´ll post here.
Thank you very much for your answers!