yugeci
- 61
- 0
Homework Statement
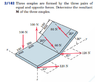
I attached the question.
Homework Equations
M = r x F
M = F x d
Resolving forces, Fx/Fy/Fz = F cos/sin theta (depending on which angle you take)
The Attempt at a Solution
I can easily find the moment of the 100 N and 120 forces, but I'm having trouble finding the moment of the 80 N force. I know we use r x F, but getting the r and F vectors is a problem for me. Here is my attempt:
Fx = -80 cos 20 = -75.18
Fy = 80 sin 20 cos 60 = 13.68
Fz = 80 sin 20 sin 60 = 23.70
F = (-75.18i + 13.68j + 23.70k)
Rx = 0, to get Ry and Rz I made a triangle with the 180mm length and 30 degree angle.
Ry = 180 cos 30 = 155.88
Rz = -180 sin 30 = -90
R = (0, 155.88, -90)
M = r x F
When I take the cross product I get = { 4923.9972, 6766.2, 11719.0584 }
While the actual answer is { 0, -6770, 1172 }
Where did I make the mistake?