mumu94
- 2
- 0
Homework Statement
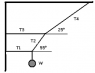
In the following diagram (see attachment), w=80N and the net force is 0.
The Attempt at a Solution
I basically made two free body diagrams and applied Net Force = 0 for each axis, obtaining 4 equations with 4 variables (T1,T2,T3,T4). I got T1=56N T2=98N T3=115N T4=189N
However, my answers are apparently completely different from the "correct ones", which are: T1=37N, T2=88N, T3=77N, T4=139N.
I would like to know whether my answers are correct or not.
Help is appreciated! Thanks!