Statics Problem: hanging disk, tensions etc.

[jstone326]

Homework Statement

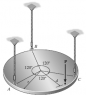
The circular plate has a weight W and a center of gravity at its center. If it is supported vy three vertical cords tied to its edge, determine the largest distance d from the center to where any vertical force P can be applied so as not to cause the force in anyone of the cables to become zero.
(see image)

Homework Equations

sum of Moments about somewhere are equal to 0

The Attempt at a Solution

I'm pretty lost as to how to start this problem. I think that I have to assume one of the tensions = 0, and that P would be located half way between C and A, thus making the angle between d and A/center = 60

Any help on how to approach this would be much appreciated.

Thanks

 

[dikmikkel]

You use Newtons 1st law first:
$T_A+T_B+T_C - mg - P = 0$
Then the sum of Torques should also be zero at the limit:
$\vec{P}\times \vec{d} + \vec{T}_A\times \vec{r_A} +\vec{T}_B\times \vec{r_B} + \vec{T}_C\times \vec{r_C} = \vec{0}$
And use that the magnitude of the cross product of two vectors x,y is given by:
$\vec{x}\times \vec{y} = |x||y|\sin(\theta)$
So the point is, be careful with signs.