Statics project: where to place a support

[musicmar]

Homework Statement

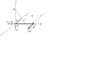
I have a project for my statics class. My topic is equilibrium of a rigid body, and I am building an assembly that will have four different support reactions. They will all be attached to one central post for ease of construction, but they will be analyzed as separate systems. I've attached a picture of what I have so far. One(only one attached so far) will have a fixed support, one a pin(using the wires attached), one a ball and socket(using kinex), and one a smooth pad. A weight will be applied from a string at the end of each "L" shaped projection. Because all except the fixed would fall over because nothing is preventing a moment about the x axis, I am also attaching a string from the top to the point where the load is applied. Three of the projections will work fine once I attach them, no matter where they are located nor what the weight is. However, the smooth pad will not work unless it is perfectly placed. I'm not exactly sure where to put it vertically on the post. I can vary the vertical placement and the weight (I'm using pennies post 1982, so multiples of 2.5 grams).

The following are the equilibrium equations for this system. I've also attached the free body diagram for the pin system. The reactions at A are not correct for the smooth pad, but the rest of the diagram is accurate.

∑Fx= 0 = Tx
∑Fy= 0 = Ty
∑Fz= 0 = -W + Tz
∑Mx= 0 = -W(b) + Tz(b)
∑My= 0 = -W(c) + Tz(c)
∑Mz= 0 = Tx(b) + Ty(c)


Thank you for your help.
~Melissa

 

[musicmar]

I've finished it now. I've attached a picture of the final product.

 

[pongo38]

I can't see where the smooth pad is. If the smooth pad is arranged to allow vertical movement, then the attachment to it must be horizontal, So can the L-shape be inclined to permit that?