Philippe
- 9
- 1
Homework Statement
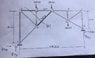
I'm having a hard time finding the support reactions R_{fx} ; R_{fy} ; R_{kx} ; R_{ky} in this truss.
2. The attempt at a solution
I got four equations using the equilibrium conditions (sum of forces along x and y ; sum of moments on F and on C) but the system doesn't seem to have a solution. Am i missing something?
<br /> (\Sigma x = 0) R_{fx} + R_{ky} = 0 \\<br /> (\Sigma y = 0) R_{fy} + R_{ky} = 530 \\<br /> (\Sigma M_{f} = 0) -8R_{kx} + 40R_{ky} = 11100 \\<br /> (\Sigma M_{c} = 0) -20R_{fx} + 20R_{fy} -12 R_{kx} - 20R_{ky} = -500<br />
Thanks!