Stick 2 Rotation: Finding Max Stability

[Knightycloud]

Homework Statement

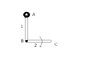
Two sticks 1 and 2 are attached together at the point B and the stick 1 is placed on point A and all these sticks can be rotated with no friction. If the stick 2 rotated freely around point B, in which direction the stick 2 will rotate?

Homework Equations

I°ω°=Iω

The Attempt at a Solution

Once I found out from another question that if these two sticks rotate at the same direction, the stability becomes the maximum.

 

[Simon Bridge]

You mean these are coupled rigid rotors (special case of pendulums)?
The pivot is at point A. Stick 2 starts horizontal and stick 1 starts vertical.
I take it gravity is not a factor here?

So stick 2 starts out with some angular momentum about point B (not it's center of mass).
What does that do to point B?

What level does this need to be done at?

 

[Knightycloud]

This is not a pendulum and these two sticks are placed vertically. If a rotation is given to BC, what will be the rotation direction of AB? I think it's the same direction as BC does. Because it gives the maximum stability to the system then. Am I right? :D

 

[Simon Bridge]

What you have described is one of the possible stationary state solutions ... but is it a solution that applies here? Have you been asked for the most stable state? Have you even been asked for a stationary state? Or are you expected to reason out the direction of rotation for stick 1 at the instant shown on the diagram?

If the two sticks are vertical - and they have mass - then it's a pendulum.
You don't have to believe me - build one and see.