xXOfNiRXx
- 13
- 0
[a]1. Homework Statement [/b]
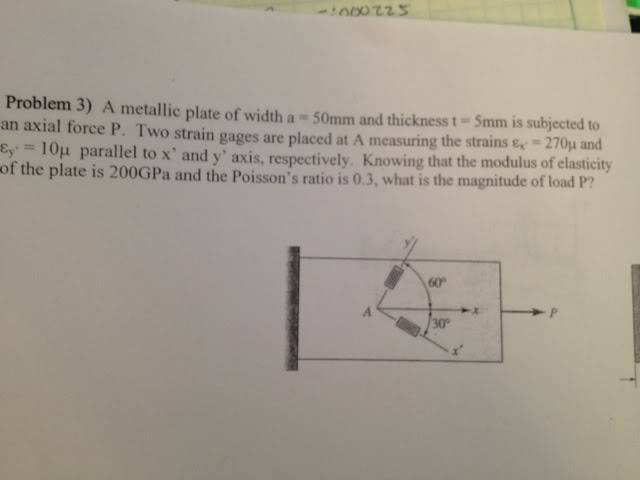
I thought it would be easier to post a picture since this way the drawing can be seen. I'm having a hard time deciding what angles to use with the relevant equations, see below.
I know that:
Ex' = (Ex/2)*(1+cos(2*theta))+(Ey/2)*(1-cos(2*theta))+(gammaxy/2)*sin(2*theta))
Ey' = (Ex/2)*(1-cos(2*theta))+(Ey/2)*(1+cos(2*theta))-(gammaxy/2)*sin(2*theta))
Gammax'y'= -Ex*sin(2*theta)+Ey*Sin(-60)+gammaxy*cos(2*theta))
Then, back solve for Ex, Ey, and gamm. Then use: Sigmaxx = (E/(1-v2))*Exx+ (v*E*Eyy)/(1-v2).
From There, Sigmax = P/A
I used -30 and 2theta = -60 for the angle in all three of the above equations. However, a friend used -30 for Ex, 60 for Ey, and 15 for gammaxy. What is the correct angle? I get 12.5KN as a final solution, while she gets 1.85KN.
I used a matrix:
Ex Ey Gammaxy = Ex' or Ey' or gammax'y' respectiveyl
.75 .25 -.433 = 270E-6
.25 .75 .433 = 10E-6
.866 -.866 .5 = 0
I find that: Ex = 250E-6 Ey=.75E-6 and gammaxy = -225E-6
I find that Sigma x = 50Mpa
and Finally P = 12.5 KN based on the above equations.
Did I make the correct assumption that I should use -30 as the angle for all three stress transformation equations? All help would be greatly appreciated. Thanks!
I thought it would be easier to post a picture since this way the drawing can be seen. I'm having a hard time deciding what angles to use with the relevant equations, see below.
Homework Equations
I know that:
Ex' = (Ex/2)*(1+cos(2*theta))+(Ey/2)*(1-cos(2*theta))+(gammaxy/2)*sin(2*theta))
Ey' = (Ex/2)*(1-cos(2*theta))+(Ey/2)*(1+cos(2*theta))-(gammaxy/2)*sin(2*theta))
Gammax'y'= -Ex*sin(2*theta)+Ey*Sin(-60)+gammaxy*cos(2*theta))
Then, back solve for Ex, Ey, and gamm. Then use: Sigmaxx = (E/(1-v2))*Exx+ (v*E*Eyy)/(1-v2).
From There, Sigmax = P/A
The Attempt at a Solution
I used -30 and 2theta = -60 for the angle in all three of the above equations. However, a friend used -30 for Ex, 60 for Ey, and 15 for gammaxy. What is the correct angle? I get 12.5KN as a final solution, while she gets 1.85KN.
I used a matrix:
Ex Ey Gammaxy = Ex' or Ey' or gammax'y' respectiveyl
.75 .25 -.433 = 270E-6
.25 .75 .433 = 10E-6
.866 -.866 .5 = 0
I find that: Ex = 250E-6 Ey=.75E-6 and gammaxy = -225E-6
I find that Sigma x = 50Mpa
and Finally P = 12.5 KN based on the above equations.
Did I make the correct assumption that I should use -30 as the angle for all three stress transformation equations? All help would be greatly appreciated. Thanks!