B Struggling to understand a consequence of Pascal's priciple

[Johnls]

Suppose there are two vessels filled with water up to the same height:

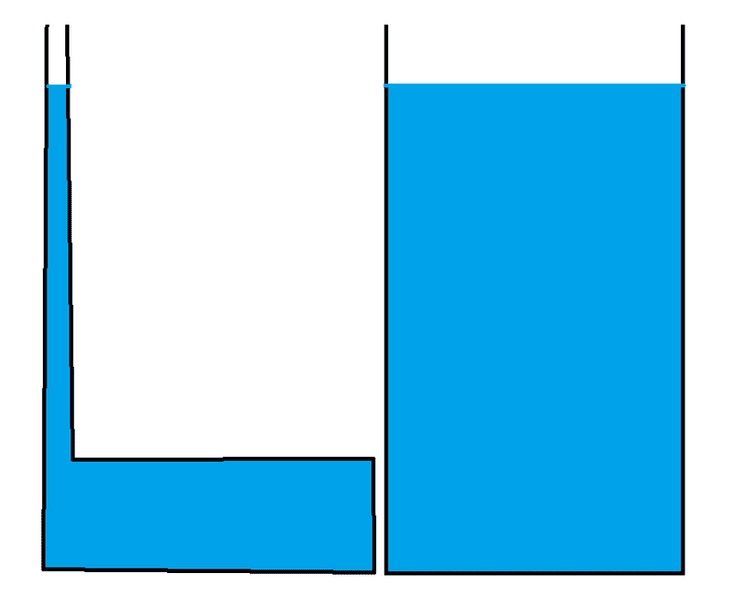
If I understand pascal's principle, the pressure in the bottom of both vessels should be the same. But the right one has more weight, so isn't the force on the bottom greater and therefore there is more pressure there?

 

[composyte]

So the point to make here is that force and pressure are not the same thing. Pascal's principle states the change in pressure is due to the change in height. However, if you try to find the change in force from the top to the bottom you will find it depends on the cross sectional area as well. As a result, the two tanks will have a very different change in force.

In short: tank on the right weighs more but they both have the same change in pressure from top to bottom.

 

[Chestermiller]

In the vessel on the left, the pressure on the horizontal "roof" section is determined by the height of the fluid in the thin section. The roof is pushing down on the liquid below with this pressure. So, if you do a force balance on the fluid in the vessel on the left, the force on the base is the same as the force on the base of the vessel on the right. This is all because, according to Pascal's law, the pressure is the same in the horizontal direction as in the vertical direction and, in this case, the pressure is constant over each horizontal surface within the fluid.

 

[Johnls]

So the point to make here is that force and pressure are not the same thing. Pascal's principle states the change in pressure is due to the change in height. However, if you try to find the change in force from the top to the bottom you will find it depends on the cross sectional area as well. As a result, the two tanks will have a very different change in force.

In short: tank on the right weighs more but they both have the same change in pressure from top to bottom.

In the vessel on the left, the pressure on the horizontal "roof" section is determined by the height of the fluid in the thin section. The roof is pushing down on the liquid below with this pressure. So, if you do a force balance on the fluid in the vessel on the left, the force on the base is the same as the force on the base of the vessel on the right. This is all because, according to Pascal's law, the pressure is the same in the horizontal direction as in the vertical direction and, in this case, the pressure is constant over each horizontal surface within the fluid.

Thanks for the quick response!
I forgot to mention that the cross sectional area of the bottom is the same in both cases. I understand how to derive that both forces are the same with Pascal's principle. What I don't understand is how can it be that if you try and calculate the pressure in a different way, by taking the weight of the water, which is a force acting on the bottom of the vessel, and divide it by the cross sectional area, you get a different pressure for each vessel. I probably made a wrong assumption somewhere, but I don't know what it is.

 

[Chestermiller]

Thanks for the quick response!
I forgot to mention that the cross sectional area of the bottom is the same in both cases. I understand how to derive that both forces are the same with Pascal's principle. What I don't understand is how can it be that if you try and calculate the pressure in a different way, by taking the weight of the water, which is a force acting on the bottom of the vessel, and divide it by the cross sectional area, you get a different pressure for each vessel. I probably made a wrong assumption somewhere, but I don't know what it is.

The force acting on the bottom of the vessel on the left is not equal to the weight of the water in the vessel. As I said, the "roof" on the right side of the vessel on the left is pushing down on the water below with just the right amount of force to compensate for the missing weight.

 

[Johnls]

The force acting on the bottom of the vessel on the left is not equal to the weight of the water in the vessel. As I said, the "roof" on the right side of the vessel on the left is pushing down on the water below with just the right amount of force to compensate for the missing weight.

I think I got it, but one more question-
Suppose I have a vessel just like the one on the left, but the wide side is 1 km^3 wide and the thick side is a few mm thick, but the thick side is 10 km long. According to Pascal's principle, there might be such a tremendous pressure to the point that the vessel will explode, right?

 

[Chestermiller]

I think I got it, but one more question-
Suppose I have a vessel just like the one on the left, but the wide side is 1 km^3 wide and the thick side is a few mm thick, but the thick side is 10 km long. According to Pascal's principle, there might be such a tremendous pressure to the point that the vessel will explode, right?

I don't quite follow exactly what you are describing. Any chance of your providing a sketch?

 

[nasu]

I think he describes something similar to Pascal's barrel.
https://en.wikipedia.org/wiki/Pascal's_barrel

 

[The Bill]

Put it this way. Imagine each vessel is being measured underneath on the outside by a scale, and at the bottom inside by a pressure gauge, and that the weight of the vessels is negligible. Assume that the platform of the scale is bigger than either vessel's bottom. The vessel on the right will weigh more, and thus apply more pressure to the scale. However, the internal pressure measured by the pressure gauges at the bottom will be the same.

 

[Johnls]

I don't quite follow exactly what you are describing. Any chance of your providing a sketch?

I think he describes something similar to Pascal's barrel.
https://en.wikipedia.org/wiki/Pascal's_barrel

This is more or less what I meant. It is just non-intuitive for me that one can get such a large impact with a little bit of water...

 

[Chestermiller]

This is more or less what I meant. It is just non-intuitive for me that one can get such a large impact with a little bit of water...

That's the principle behind the hydraulic lift. Google "hydraulic lift principle."

 

[The Bill]

This is more or less what I meant. It is just non-intuitive for me that one can get such a large impact with a little bit of water...

In a real system, the lower barrel will have a finite elasticity. The actual amount of water you have to add to the small tube above the barrel could end up being rather a lot more than the volume of the tube alone, since you have to add enough to account for the stretched volume of the barrel at the higher pressure.

For a simple experiment illustrating this, imagine (Or actually do! This one's easy with some cheap supplies from the hardware store.) a rubber balloon attached to the end of a piece of tubing by a hose clamp. As the length of tubing above the balloon increases, one has to add a lot more fluid to get to a given height because the increased pressure expands the balloon quite a bit.

 

[jbriggs444]

For a simple experiment illustrating this, imagine (Or actually do! This one's easy with some cheap supplies from the hardware store.) a rubber balloon attached to the end of a piece of tubing by a hose clamp. As the length of tubing above the balloon increases, one has to add a lot more fluid to get to a given height because the increased pressure expands the balloon quite a bit.

Note that as a balloon is inflated, the pressure increase with radius is quite gradual. The increasing tension in the balloon material and the decreased curvature in the balloon's surface combine so that the net effect is nearly a wash. It is possible for pressure to actually decrease as fluid is added. Chestermiller has participated in a number of threads over the years involving such situations.

 

[The Bill]

--snip--

Right. For that reason it fits work better with a larger, heavier gauge balloon, taking care not to load it past its nonlinear point. The experiment might work well with a specially constructed "barrel" designed to behave in a more controlled fashion within a linear regime. Perhaps a short large diameter piece of transparent PVC pipe with a piston and a spring.

 

[Chestermiller]

In my judgment, The Bill's response regarding the elastic response of the container is irrelevant to the question posed by the OP regarding hydrostatics, and only serves to cloud the issue.

 

[The Bill]

In my judgment, The Bill's response regarding the elastic response of the container is irrelevant to the question posed by the OP regarding hydrostatics, and only serves to cloud the issue.

My point is that in response to Johnls saying "that one can get such a large impact with a little bit of water.." it really isn't just "a little bit of water" in practice.

 

[Chestermiller]

My point is that in response to Johnls saying "that one can get such a large impact with a little bit of water.." it really isn't just "a little bit of water" in practice.

He was referring to the little bit of water in the thin vertical pipe to the left.

 

[The Bill]

He was referring to the little bit of water in the thin vertical pipe to the left.

I know.

The thought experiment I used above is, however, exactly what helped me get past the intellectual hurdle of understanding this situation in hydrostatics. If it worked for me, it might help someone else, and I do not believe you are correct in declaring it irrelevant, from a pedagogical standpoint. If it helps a single person, it is not pedagogically irrelevant. It helped me. I ma at least a single person. Ergo, you were incorrect in declaring it irrelevant, if you meant "pedagogically irrelevant."

 

[Chestermiller]

I know.

The thought experiment I used above is, however, exactly what helped me get past the intellectual hurdle of understanding this situation in hydrostatics. If it worked for me, it might help someone else, and I do not believe you are correct in declaring it irrelevant, from a pedagogical standpoint. If it helps a single person, it is not pedagogically irrelevant. It helped me. I ma at least a single person. Ergo, you were incorrect in declaring it irrelevant, if you meant "pedagogically irrelevant."

As a Mentor at physics forums, it is my responsibility to reach decisions regarding the relevance of answers, based on my judgment as to whether the answers will likely help the member or whether they will confuse him even further. I have been selected as a Mentor and have been endowed with that power based on the technical competence I have historically demonstrated at this site. I regard your responses as bordering on misinformation. Now, if you continue to persist with this, I will be forced to issue you infraction points for misinformation and to delete the offending posts. Eight infraction points earns you a temporary ban and 10 infraction points earns you a permanent ban.

Chet

 

[gmax137]

It seems to me, the issue is this:

for a 'regular' shaped tank, where all of the liquid is at the same level, the pressure at the bottom of the tank times the area of the bottom = the total weight of the liquid.

for the 'odd' shaped tank, this isn't true. In fact the pressure times the area can be much greater than the weight of the liquid. And yet, the floor that the tank sits on, feels only the total weight.

 

[jbriggs444]

[...]And yet, the floor that the tank sits on, feels only the total weight.

Which means that the net force on the bottom of the container from the fluid above does not match the net force on the bottom of the container from the support below. I guess it is a good thing that the container is rigid...