How to Prove Vector Ratios BE:EF = 1:2 and CD:DF = 1:1?

[Warr]

Hmm...having a problem with a proof here:

http://www.cuneo.us/tesmw/images/Warr/untitled.JPG

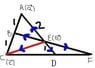
the information given is in the picture

I have to prove that BE:EF = 1:2, and also that CD:DF = 1:1

sorry if it is drawn badly, I did it quickly..but you get the idea.

This needs to be a vector proof. So I'm assuming it has to have something to do with linear independence, thought I don't exactly know how to do it. I'd appreciate if anyone could help me out.

 

[himanshu121]

It won't help if i solve this problem for u

So i give u some hints which will start ur quest

Consider E as your origin With A and C as Position vectors(PV) a and b {bold represents vectors} write PV for B using section formula PV for D will be -a/2

Assume the ratio DF/CD=m and similarly for FE/EB=n

Now again using section formula find PV in terms of m And then in terms of n

Equate the two PV thus obtained And i hope u ur Q. will be concluded

 

[Warr]

I still can't get it :(

I really want to know how to do this...Can someone please just give me the full answer. I really think I'm missing something big here.

 

[Warr]

*Bump*

This is getting kind of urgent...I need to know this for a test tomorrow and I have no idea how to do it! =(

 

[Warr]

Sorry about all this bumping...but I am in dire need. Please, I'm begging someone to finish this >_<

 

[himanshu121]

Ok have u tried The hints i have given

 

[himanshu121]

Consider E as origin And PV of A(a) and C(c) where a and c are PV



now from section formula
PV of B(b)

\mbox{<b>b</b>} = \frac{\mbox{<b>a</b>}+\mbox{<b>c</b>}}{2} and note the direction as well

Also PV for D(d) = - a/2 note down the direction

now consider the ratio CD:DF=1:m

Again from section formula PV for D is given by
=\frac{\mbox{<b>f</b>}+m\mbox{<b>b</b>}}{m+1} = - \frac{\mbox{<b>a</b>}}{2}

After rearrangement u get
f= -(m+1)a/2 - mb ...1

Similarly consider BE:EF=1:n

for which PV of F
(\mbox{<b>f</b>}) = n\mbox{<b>b</b>}=n \frac{\mbox{<b>a</b>}+\mbox{<b>c</b>}}{2} ...2

Equatin 1 and 2
u get

\frac{n\mbox{<b>a</b>]}{2}+\frac{n\mbox{<b>b</b>}}{2}=-\frac{(m+1)\mbox{<b>a</b>}}{2} - m\mbox{<b>b</b>}
Now from the properties of vectors or say uniqueness

We have
n=-(m+1) ...3
and n=-2m ...4

from 3&4
m=1 i.e CD:DF=1:1
n=2 i.e BE:EF=1:2

 

[himanshu121]

Here is the attachment for fig