Amaelle
- 309
- 54
- Homework Statement
- look at the image below
- Relevant Equations
- asymptotic behaviour, limit of partial sum
Greeting
I'm trying to study the convergence of this serie

I started studying the absolute convergence
because an≈n^(2/3) we know that Sn will be divergente S=∝ so arcatn (Sn)≤π/2 and the denominator would be a positive number less than π/2, and because an≈n^(2/3) and we know 1/n^(2/3) > 1/n so we conclude that this serie divergent (not absolutely convergent till this point)
but here is the solution of the book
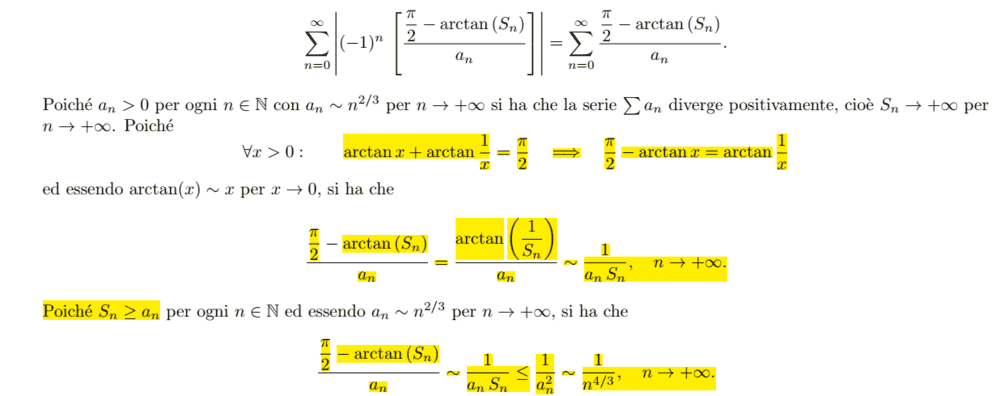
so according to them the serie is absolutely convergent
I would be grateful if someone could explain me where I get wrong in my reasoning
Many thanks in advance!
Best
I'm trying to study the convergence of this serie
I started studying the absolute convergence
because an≈n^(2/3) we know that Sn will be divergente S=∝ so arcatn (Sn)≤π/2 and the denominator would be a positive number less than π/2, and because an≈n^(2/3) and we know 1/n^(2/3) > 1/n so we conclude that this serie divergent (not absolutely convergent till this point)
but here is the solution of the book
so according to them the serie is absolutely convergent
I would be grateful if someone could explain me where I get wrong in my reasoning
Many thanks in advance!
Best