Firepanda
- 425
- 0
I've created two summations for my coursework, now I need to show whether or not the summations are finite or infinite.
The 2 summations are very similar:
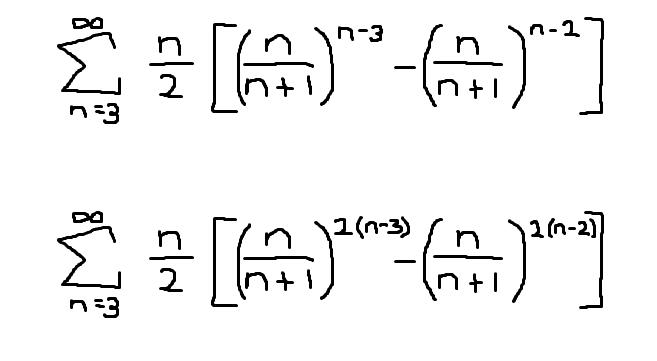
With the n/2 removed it was easy enough to show the sum was equal to 1 [edit: I now realize I may have this wrong], now with the n/2 term added I really have no idea where to start.
Any help appreciated, thanks.
Edit: I can see my writing may not be legible, 1's in the pic are straight vertical lines, some of the 2's may look like 1's, but they are 2's.
The 2 summations are very similar:
With the n/2 removed it was easy enough to show the sum was equal to 1 [edit: I now realize I may have this wrong], now with the n/2 term added I really have no idea where to start.
Any help appreciated, thanks.
Edit: I can see my writing may not be legible, 1's in the pic are straight vertical lines, some of the 2's may look like 1's, but they are 2's.
Last edited: