Super elastic collision between two objects

AI Thread Summary
The discussion revolves around a physics problem involving a super elastic collision between two masses, m1 and m2, with specific parameters provided. The user initially struggles with calculations related to momentum and kinetic energy conservation, particularly in determining the velocity required for mass m2 to reach a designated point. Key insights include applying the conservation of energy to find the necessary speed for m2 and understanding how the spring's force affects m1's velocity. Ultimately, the user successfully calculates the compression distance of the spring, concluding with a value of 5.8 cm. This highlights the importance of energy conservation and kinematic principles in solving collision problems.
noffya
Messages
5
Reaction score
0
Hello,
I have difficulties with this problem:

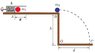
The body mass m1 = 20 g is fired with a spring, k = 72 N / m from position A. On arrival at point B hits completely elastic body mass m2 = 15 g.

Find the distance x of compressed spring so that the mass m2 reaches point C separated a distance d = 90 cm from point O. Data: h = 25 cm.

I was trying to do the calculations and camera up with these:
Since momentum P and cinetic energy are constant therefore m1*v0=m1v1+m2v2 and 1/2m1v0=1/2m1v1 +1/2m2v2
To find the v2 of the object m2 I apply conservation of energy law and it sums up to 1/2m2v2 = m2gh

After making calculations I get stuck and I think I'm missing something.
Please give an advice with this.
Thanks
 

Attachments

  • 1389455371034.jpg
    1389455371034.jpg
    18.3 KB · Views: 511
Physics news on Phys.org
Ask yourself: How fast must m2 have been going to land at point C?
 
Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed
 
oneplusone said:
Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed

Doc Al said:
Ask yourself: How fast must m2 have been going to land at point C?
Thanks for hints!
 
oneplusone said:
Here are some useful things which I will leave for you to find (if you get stuck, ill show you how).

1. How fast does m2 have to go? (Kinematics)
2. If m2 has to go "v" meters per second, how fast would m_1 need to go right before they collide?
3. F=-kx, and F=ma, so the spring provides an acceleration to m_1 when released. How does this affect m1's speed

Got it. I applied energy conservation law at step 3 and got the x equals 5.8cm
Thanks a lot!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Figure 1 Overall Structure Diagram Figure 2: Top view of the piston when it is cylindrical A circular opening is created at a height of 5 meters above the water surface. Inside this opening is a sleeve-type piston with a cross-sectional area of 1 square meter. The piston is pulled to the right at a constant speed. The pulling force is（Figure 2）： F = ρshg = 1000 × 1 × 5 × 10 = 50,000 N. Figure 3: Modifying the structure to incorporate a fixed internal piston When I modify the piston...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Elastic Collision and Momentum of Ice Skaters
Replies
16
Views
3K
Question about two elastic collision formulas
Replies
6
Views
2K
Elastic collision between two balls with different masses
Replies
8
Views
5K
How do I solve for an elastic collision going up a ramp?
Replies
10
Views
3K
Why Is the Angle 90 Degrees in Elastic Collisions of Equal Mass?
Replies
10
Views
5K
Kinetic energy and momentum in an elastic collision
Replies
22
Views
3K
Solving Elastic Collision of Two Balls: Theory & Solutions
Replies
15
Views
3K
Physics Help with elastic collision
Replies
5
Views
2K
Elastic collision heavy particle problem
Replies
12
Views
3K
Conservation of Momentum (elastic collision of masses)
Replies
15
Views
7K

Hot Threads

Recent Insights

Back
Top