bananabandana
- 112
- 5
Homework Statement
I'm looking at an E&M textbook - "Time-Harmonic Electromagnetic Fields". They state:
"A more general ##x ## polarized field is one consisting of waves traveling in opposite directions with unequal amplitudes - i.e :
(1) $$ E_{x} = Ae^{-jkz} +Ce^{jkz}$$
Let ## A ## and ##C## be real. We express the field in terms of an amplitude and phase. This gives:
(2) $$E_{x} = \sqrt{A^{2}+C^{2}+2ACcos(2kz)} \ e^{-jtan^{-1} \bigg( \frac{A-C}{A+C} tan(kz) \bigg) } $$"
(1) $$ E_{x} = Ae^{-jkz} +Ce^{jkz}$$
Let ## A ## and ##C## be real. We express the field in terms of an amplitude and phase. This gives:
(2) $$E_{x} = \sqrt{A^{2}+C^{2}+2ACcos(2kz)} \ e^{-jtan^{-1} \bigg( \frac{A-C}{A+C} tan(kz) \bigg) } $$"
But I can't see where this comes from.
Homework Equations
The Attempt at a Solution
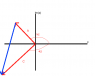
It would have though that amplitude is coming out of a cosine rule - that there is a vector triangle with ##\vec{A}## and ##\vec{C}## as two sides. In the argand/phasor diagram, the angle between ##Ae^{-jz} ## and ##Ce^{jz}## is going to be fixed (for any given time) as ##2kz## (or ## 2\pi -2kz ##) So by applying the cosine rule, I'd expect:
$$ |E_{x}| = |A|^{2}+|C|^{2} -2|A||C|cos(2kz) $$
But in the book there is a plus. Is this a typo, or have I messed up?
and I can get the phase from just expanding out ##E_{x} ## into components - from (1):
$$E_{x}= (A+C) cos(kz) + j(C-A)sin(kz)$$
So if we want to write ## E_{x} ## as: $$E_{x} = |E_{x}| e^{j\phi} = |E_{x}| (cos\phi + jsin\phi)$$ Then:
$$ tan(\phi) = \frac{C-A}{A+C} tan(kz) \implies tan(-\phi) = \frac{A-C}{A+C} tan(kz), \therefore \phi =-tan^{-1}\bigg(\frac{A-C}{A+C} tan(kz) \bigg) $$
If that second bit is right - is the reason that we can't equate amplitude of that equation with the book amplitude because we have ignored time dependence? Just started doing this, so any help is appreciated.
Thanks :)