pgetts
- 11
- 1
1. Homework Statement .
Figure 1 shows a 50 Ω load being fed from two voltage sources via their associated reactances. Determine the current i flowing in the load by:
(a) Thevenin's theorem
(b) Superposition
(c) Transforming the two voltage sources and their associated reactances into current sources( and thus forming a pair of Norton genorators
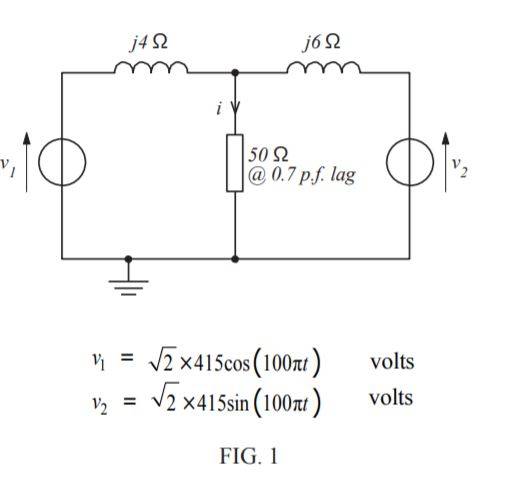
V1 = √2 x 415cos(100pit) ∴ 415∠90 RMS
∴ j415 as cos leads sin by 90 degress.
V2 = √2 x 415sin(100pit) ∴ 415∠0 RMS
∴ 415
ZL = 50Ω @ 0.7 P.F ... convert into polar
sin-1 0.7 = 45.573 degrees
∴ 50∠45.573 convert into rectangular.
∴ 34.999+j35.7072. Homework Equations
Kirchhoffs voltage law.
Superposition
Cramers Rule3. The Attempt at a Solution
So, so far my process is to discard one of the voltage sources (V2)
Work out the two loop equations and using V1 and then using Cramers Rule I get the below matrix's (Δ, Δ1, Δ2)
Δ
Loop 1 = -j4(I1) -35.002+j35.705(I2) = -j415 eq 1
Loop 2 = -j6(I1) 35.002+j41.705(I2) = 0 eq 2
Now following Cramers rule I get Δ= (-j4)(35.002+j41.705) - (-j6)(-35.002+j35.705)
Δ= (166.82-j140.008)-(214.23+j210.012)
Δ= -47.41-j350.02
Δ1 Matrix
-j415 -35.002+j35.705
0 35.002+41.705
Δ1 = -14525.8-j17307.6
Δ2 Matrix
-j4 -j415
-j6 0
Δ2=2490
And I2 would equal Δ2/Δ
And so on for the whole process again for the second voltage.
Then sum I2 from voltage source one minus I2 from voltage source 2.
My problem is my superposition is not correct and I cannot see where my mistake is.
I'm confident that my Thevenin's is correct. 5.714+j0.892A or 5.783∠8.872 Deg's as I also have this as my answer using Nortons.
Figure 1 shows a 50 Ω load being fed from two voltage sources via their associated reactances. Determine the current i flowing in the load by:
(a) Thevenin's theorem
(b) Superposition
(c) Transforming the two voltage sources and their associated reactances into current sources( and thus forming a pair of Norton genorators
V1 = √2 x 415cos(100pit) ∴ 415∠90 RMS
∴ j415 as cos leads sin by 90 degress.
V2 = √2 x 415sin(100pit) ∴ 415∠0 RMS
∴ 415
ZL = 50Ω @ 0.7 P.F ... convert into polar
sin-1 0.7 = 45.573 degrees
∴ 50∠45.573 convert into rectangular.
∴ 34.999+j35.7072. Homework Equations
Kirchhoffs voltage law.
Superposition
Cramers Rule3. The Attempt at a Solution
So, so far my process is to discard one of the voltage sources (V2)
Work out the two loop equations and using V1 and then using Cramers Rule I get the below matrix's (Δ, Δ1, Δ2)
Δ
Loop 1 = -j4(I1) -35.002+j35.705(I2) = -j415 eq 1
Loop 2 = -j6(I1) 35.002+j41.705(I2) = 0 eq 2
Now following Cramers rule I get Δ= (-j4)(35.002+j41.705) - (-j6)(-35.002+j35.705)
Δ= (166.82-j140.008)-(214.23+j210.012)
Δ= -47.41-j350.02
Δ1 Matrix
-j415 -35.002+j35.705
0 35.002+41.705
Δ1 = -14525.8-j17307.6
Δ2 Matrix
-j4 -j415
-j6 0
Δ2=2490
And I2 would equal Δ2/Δ
And so on for the whole process again for the second voltage.
Then sum I2 from voltage source one minus I2 from voltage source 2.
My problem is my superposition is not correct and I cannot see where my mistake is.
I'm confident that my Thevenin's is correct. 5.714+j0.892A or 5.783∠8.872 Deg's as I also have this as my answer using Nortons.
Attachments
Last edited by a moderator: