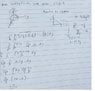- #1
chetzread
- 801
- 1
Homework Statement
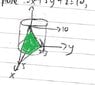
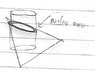
Find the surface portion bounded by plane 2x +5y + z = 10 that lies in cylinder (x^2) +(y^2) = 9 ...
I have skteched out the diagram and my ans is 5sqrt(30) instead of 9sqrt (30) as given by the author ...
Anything wrong with my working ?