Salazar
- 8
- 0
Homework Statement
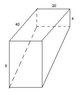
A swimming pool is 40 feet long, 20 feet wide, 4 feet deep at the shallow end, and 9 feet deep at the deep end. Water is being pumped into the pool at 10 cubic feet per minute.
a. When the water is 3 feet deep at the shallow end, at what rate is the water level rising? b. When the water is 3 feet deep at the deep end, at what rate is the water level rising?
Homework Equations
None Given.
The Attempt at a Solution
I had [dV/dt] and the volume for part a is V = L*W*H and I had L and W, which were 40' and 20' respectively. So V = 800H and I used implicit differentiation to get [dV/dt] = 800[dH/dt], so [dH/dt] = 1/80 feet per minute.
For part be it seems straightforward, but I do not know how to get the length, since it has change. Picture of the pool is uploaded.
Attachments
Last edited: