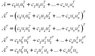Symmetric matrix with eigenvalues

[Ylle]

Homework Statement

Let {u₁, u₂,...,u_n} be an orthonormal basis for Rⁿ and let A be a linear combination of the rank 1 matrices u₁u₁^T, u₂u₂^T,...,u_nu_n^T. If

A = c₁u₁u₁^T + c₂u₂u₂^T + ... + c_nu_nu_n^T

show that A is a symmetric matrix with eigenvalues c₁, c₂,..., c_n and that u_i is an eigenvector belonging to c_i for each i.

Homework Equations

No clue...

The Attempt at a Solution

I'm really stuck with this problem. So I'm really just hoping for a little hint or something.
It SOUNDS easy, but as I said, I have no clue where to start.

Hope you can help.


Regards

 

[tiny-tim]

Hi Ylle!

… show that A is a symmetric matrix with eigenvalues c₁, c₂,..., c_n and that u_i is an eigenvector belonging to c_i for each i.

(i assume you can prove that A is symmetric)

You just need to prove that Au_i = c_iu_i

(and remember the basis is orthonormal )

 

[Ylle]

Hi :)

I'm not totally sure about the first, but I have this (See the picture added). I don't know if it is proved there ?
For it to be symmetric it's it has to be: A = A^T, right ?

And the next I can't figure out what you mean :?
If you add u_i to A I guess you can remove the u_1-n and u_1-n^T because they become the identitymatrix for all of them. And then you have c_1-nu_i left. So how do I make the c_1-n to c_i ? :)

 

[tiny-tim]

I'm not totally sure about the first, but I have this (See the picture added). I don't know if it is proved there ?
For it to be symmetric it's it has to be: A = A^T, right ?

Hi Ylle!

Yes, A = A^T.

But your proof doesn't work, because transpose is like inverse … it alters the order of things … so (AB)^T = B^TA^T

And the next I can't figure out what you mean :?

Just write Au_i in full (using the orthonormality of the u's) …

what do you get?

 

[Ylle]

Well, my guess is you have:

A = c_iu_iu_i^T

If you then add u_i on both sides you get:

Au_i = c_iu_iu_i^Tu_i

And because u_iu_i^T = <u_i,<u_i> = ||u_i|| = 1 since it's a basis, you have:

Au_i = c_iu_i


Don't know if that is correct ?

 

[tiny-tim]

Hi Ylle!

(btw, please don't say "add" … say "multiply", or if you prefer a more neutral word, "apply" )

… And because u_iu_i^T = <u_i,<u_i> = ||u_i|| = 1 since it's a basis, you have:

Au_i = c_iu_i

Don't know if that is correct ?

Yup, that's fine …

that's what "orthonormal" is all about!

but … you still have to deal with all the u's in the ∑ that aren't that particular u_i …

use the orthonormal property again.