- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
Let $F\subseteq \mathbb{R}^2$. A map $\pi:\mathbb{R}^2\rightarrow \mathbb{R}$ is called symmetry map of $F$, if $\pi(F)=F$. A symmetry map of $F$ is a map where the figures $F$ and $\pi (F)$ are congruent.
I have done the following:
Let $F\subseteq \mathbb{R}^2$. A map $\pi:\mathbb{R}^2\rightarrow \mathbb{R}$ is called symmetry map of $F$, if $\pi(F)=F$. A symmetry map of $F$ is a map where the figures $F$ and $\pi (F)$ are congruent.
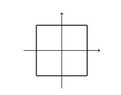
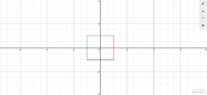
- Let $\pi_1:\mathbb{R}^2\rightarrow \mathbb{R}^2$, $x\mapsto \begin{pmatrix}0 &-1 \\ 1 & 0\end{pmatrix}\cdot x$ and $\pi_2:\mathbb{R}^2\rightarrow \mathbb{R}^2$, $x\mapsto \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\cdot x$ be symmetry maps of the below square:
View attachment 9530
- Determine the mapping formula of $\pi_1\circ \pi_2$ and $\pi_2\circ\pi_1$. Give the geometric interpretation of $\pi_1, \ \pi_2, \ \pi_1\circ \pi_2, \ \pi_2\circ \pi_1$.
- Describe all other symmetry maps of the square geometrically and give the mapping formula in each case.
- Show that all symmetry maps of the square can be represented by executing $\pi_1$ and $\pi_2$ one after the other.
- Let $\delta_a:\mathbb{R}^2\rightarrow \mathbb{R}^2$, $x\mapsto d_a\cdot x$ be a rotation by $a$ anticlockwise around the origin.
- Determine $\delta_a\left (\begin{pmatrix}1 \\ 0\end{pmatrix}\right )$ and $\delta_a\left (\begin{pmatrix}0 \\ 1\end{pmatrix}\right )$. Make a graph for that.
- Determine $d_a$.
- Show that $\delta_a\circ \delta_b=\delta_{a+b}$.
I have done the following:
-
- For $\pi_1\circ \pi_2$ we have:
\begin{equation*}\left (\pi_1\circ \pi_2\right )(x)=\pi_1 \left (\pi_2(x)\right )=\pi_1 \left (\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\cdot x\right )=\begin{pmatrix}0 &-1 \\ 1 & 0\end{pmatrix}\cdot \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\cdot x=\begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}\cdot x\end{equation*}
For $\pi_2\circ \pi_1$ we have:
\begin{equation*}\left (\pi_2\circ \pi_1\right )(x)=\pi_2 \left (\pi_1(x)\right )=\pi_2 \left (\begin{pmatrix}0 &-1 \\ 1 & 0\end{pmatrix}\cdot x\right )=\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\cdot \begin{pmatrix}0 &-1 \\ 1 & 0\end{pmatrix}\cdot x=\begin{pmatrix}0 & -1 \\ -1 & 0\end{pmatrix}\cdot x\end{equation*}
For the geometric interpretation we have to see graphically what the map does at the unit vectors, or not? (Wondering) - Could you give a hint for that? (Wondering)
- Could you give me a hint how we could show that? (Wondering)
- For $\pi_1\circ \pi_2$ we have:
- How can we do that without knowing $d_a$ ? (Wondering)
- How can we determine $d_a$ ? (Wondering)