I Taking Projectile Motion to make Planetary Trajectories

[10Exahertz]

Hi all I have been trying to find A set of equations that can allow me to map the movement of a planetary body on a polar coordinate sheet (a 2-D Problem). As well as allow me to find out about information such as the perigee and apogee radaii.
So far i have been using Keplers equations and guessing the eccentricity of the orbit. But that is not really a good way of approaching it. However, I couldn't figure out how to do it with Keplers equations so I turned to Projectile Motion. I am currently trying to figure out how to use the basic projectile motion diff eq to map a planets orbital trajectory. Only problem I haven't tried to account for yet is that the normal projectile motion equations seem to assume a flat earth.
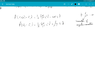
I have attached a screenshot of some of my work.

 

[sophiecentaur]

It's pretty easy to apply Newton's gravitational law and the Second law of motion (any co ordinates you want) and do a step by step approach to give an animation. Start with a given velocity and position and apply the gravitational acceleration over a short time Δt. That gives you another position and velocity. The piecewise linear approach will introduce a small error but reducing the step size can reduce it as much as you want.
Re "flat Earth"; the acceleration you need is not constant g (flat Earth) but GM/r², directed along the radius from the Sun. I did this on a Psion 3a, many years ago with a compiled 'Basic' language. You could leave it running for a long time before the orbit precessed noticeably. It's not a very sophisticated method by you can find perigee and apogee easily enough by finding the turning values of r.

 

[10Exahertz]

Well I created an equation but its implicitly defined. I am not sure if the computer would have a problem with this. But I do considering i would like to be able to map this out without the assistance of a computer.
Here is what I have gotten so far(linked image), but maybe I am overthinking the simplification. Any help in simplifying this so its only dependent on r would be helpful.