Tangential Acceleration of park ride

[Peach]

Homework Statement

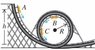
A car in an amusement park ride rolls without friction around the track shown in the figure View Figure . It starts from rest at point A at a height h above the bottom of the loop. Treat the car as a particle.

If the car starts at height h = 72.0 m and the radius is R = 16.0 m, compute the tangential acceleration of the passengers when the car is at point C, which is at the end of a horizontal diameter.

Homework Equations

Don't know...

The Attempt at a Solution

This is part of a problem and I've already solved the first three. I have the radial acceleration, the velocity at B, and the velocity at C. But I don't know how to find the tangential acceleration at C. I've tried Newton's laws already to find the acceleration so that I can use a^2 = a_rad^2 + a_tan^2 but I don't have time or distance between C and B. Can someone pls give me a nudge in the right direction? I've been struggling over this problem for two hours already. ><

 

[cycam]

Hey, how did you get Part A? I have managed to get the other parts except for the Tangential Acc part but I'm working on it and making sure my calculations are right. When i get it i'll tell you how I got it but can you help me with the first part?

 

[Peach]

How did you get the other parts without doing part A?

Use the conserved energy law. K_1 + U_1 = K_2 + U_2 right? Point 1 should be at the top of the roller coaster with height h. Point 2 should be at B. Then just plug and chug. ^^

 

[cycam]

it's late lol, soo my mind is working in funky mode. while waiting I did part a lol. Going to do part D now, but might get back to it tomorrow. tired x_x

 

[Peach]

I understand. ^^; I'm not getting any of this stuff either. Been stuck on a problem for hours already. Going to post it now.

 

[Peach]

BUMP. Pls help...still stuck, it's not getting through. :x

 

[cycam]

Ok, what is the exact definition of Tangential Acceleration?

I spent about an hour researching to see if I could find an formula and I found one but when I found the answer I realized it was right under my nose the whole time.

*hint: You didn't post all the information in the problem. The missing information is the key to finding the answer.

 

[Peach]

I didn't post part A right? But what does the minimum height have to do with this...? I found a formula for tangential acceleration too, not sure if it's the same as yours too. It's r*alpha but I can't apply that to this. At least I don't think so. o_o

Uh tangential acceleration, it's in the direction of the velocity vector, that's how the speed increase.

 

[cycam]

If the car starts at height h = 60.0 m and the radius is R = 15.0 m, compute the tangential acceleration of the passengers when the car is at point C, which is at the end of a horizontal diameter.
Take the free fall acceleration to be g = 9.80 m/s^2.

That is my question.

The Tangential Acceleration is down, the normal force at point C is horizontal, there is no friction so the only downward force is gravity.

Like i said, the missing piece of information is the key to the answer. I spent sooo much time looking at the complexity that I forgot the base of physics will always be the simplicity.

 

[Peach]

Omg, the missing piece you were talking about was the gravity acceleration. I thought it was the height. Eh. This officially makes me feel very very dumb. o_o But yeah, thanks for helping me. I spent so much time on this problem too. ><

 

[cycam]

No need to feel dumb, it took me HELLA long to figure that out lol. It wasn't until my boyfriend pointed that out that I realized what it was ha ha. I always forget not to overlook the obvious things in focus on the complexity