magnas
- 3
- 0
Hi,
I am reviewing a problem with the associated solution and there is something i don t understand.
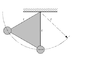
Imagine a triangle with vertices l, masses m are attached to the two end of the vertices and on the top end vertice there is a pivot so that the triangle can swing. We start with the triangle at rest and one of the rod is vertical.
Question: what is the accelerations of the masses (the two following words are in italics) just after it is released?
What i don t understand is the following:
"since v=0 at the start , the radial accelerations are zero"(quote from the solution). And then, the problem is treated as there is no radial acceleration at all, while considering a tangential acceleration. How can we consider a tangential acceleration without a radial/centripetal acceleration?
If this is possible, could you explain me and clarify with an example?
Thank you.
I am reviewing a problem with the associated solution and there is something i don t understand.
Imagine a triangle with vertices l, masses m are attached to the two end of the vertices and on the top end vertice there is a pivot so that the triangle can swing. We start with the triangle at rest and one of the rod is vertical.
Question: what is the accelerations of the masses (the two following words are in italics) just after it is released?
What i don t understand is the following:
"since v=0 at the start , the radial accelerations are zero"(quote from the solution). And then, the problem is treated as there is no radial acceleration at all, while considering a tangential acceleration. How can we consider a tangential acceleration without a radial/centripetal acceleration?
If this is possible, could you explain me and clarify with an example?
Thank you.