darkshadow28
I have to do a Taylor expansion of the energy levels of Dirac's equation with a coulombian potential in orders of (αZ/n)^2 , but the derivatives I get are just too large, I guess there is another approach maybe?
This is the expression of the energy levels
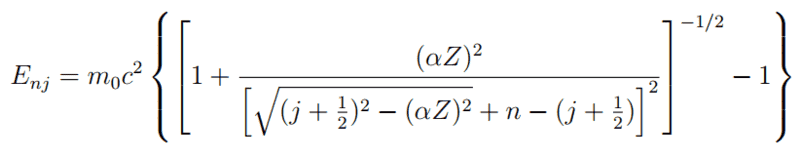
And i know it has to end like this:
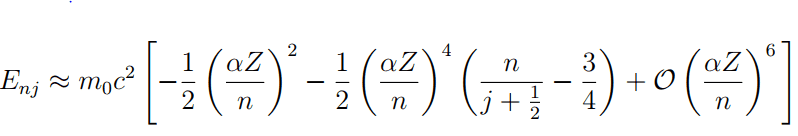
This is the expression of the energy levels
And i know it has to end like this: