Temperatures of the hot source and cold sink in a heat engine

[FranzDiCoccio]

Hi,
I was just wondering about the efficiency of a cycle that is not Carnot cycle.

In that case one should use $\eta = 1-\left|\frac{Q_{\rm out}}{Q_{\rm in}}\right|$, where $Q_{\rm in}$ and $Q_{\rm out}$ are the amounts of heat absorbed and released during the cycle.

For instance, I guess that in an (ideal) Stirling cycle (isochoric - isothermal expansion - isochoric - isothermal compression) $Q_{\rm in}$ involves the isochoric transformation with increasing temperature and the isothermal expansion, while $Q_{\rm out}$ involves the remaining two transformations.
I quickly browsed online and I actually found something like that.

Now the usual diagram for a generic machine (at least in my textbook) seems to suggest that $Q_{\rm in}$ is absorbed from a heat resevoir at some temperature $T_h$ and $Q_{\rm out}$ released into a heat sink at a lower temperature $T_c<T_h$.
See e.g. this one I found on the web, which is similar to the ones in my textbook

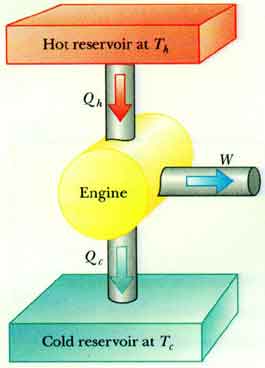But, in the case of the Stirling cycle, what does it really mean that $Q_{\rm in}=Q_{\rm isothermal}+Q_{\rm isochoric}$ is absorbed "at $T_h$"? It seems to me that this could apply to the isothermal part only, because the heat intake in the isochoric process does not happen at a fixed temperature...Are all of these diagrams actually referring to a Carnot engine?
Or perhaps this has to do with the fact that any cycle can be decomposed into many Carnot cycles, so ultimately the diagrams assume that the heat exchanges happen at fixed temperatures?

Thanks a lot for any insight.
Franz

 

[mfig]

In a Stirling cycle, the only heat added from the hot reservoir is during the isothermal process at $T_H$, while all the heat rejected to the cold reservoir would take place during the other isothermal process at $T_L$. The heat interactions during the isochoric processes are internal - i.e., from heat stored in and taken from the regenerator. Heat rejected to the regenerator during the isochoric cooling is absorbed during the iscochoric heating. These heat interactions do not see the thermal reservoirs. Note this assumes the regenerator is 100% efficient.

 

[FranzDiCoccio]

Hi mfig,
thanks for your reply and the interesting insight.

My doubt was much more basic, though. The Stirling cycle was just an example. Any non-Carnot cycle would have done.

I was focusing on the (high school) textbook diagrams, and I thought that the two temperatures of the reservoirs should refer to the thermodynamic cycle too. Hence I could not understand how a transformation that is not isothermal could happen at a fixed temperature.

Now I see I was thinking it wrong, and it seems to me that I have a clearer picture.
The temperatures of the heat exchanges do not refer to the individual transformations in the cycle.
They refer to the reservoirs which, by definition, (ideally) are systems capable of exchanging any amount of heat while keeping their temperature unchanged.

In a cycle, heat can be absorbed from a reservoir at a fixed temperature during any transformation, no matter if isothermal or not. If the process is not isothermal, this will cause an increase of temperature of the working substance.

Thanks again
Francesco