Does efficiency always depend on reversibility of the engine?

[Soren4]

I'm confused on the efficiency of a Thermal engine in the case it is reversible or not reversible, in particular where the ideal gas follows isochoric or isobaric processes.

Infact during isochoric and isobaric processes $$Q_{isochoric}=n c_v \Delta T$$
$$Q_{isobaric}=n c_p \Delta T$$

So the heats depend only on the temperatures and not on the process. So it really seems to me that the reversibility or irreversibility does not change the efficiency at all. Consider the cycle in the diagram, made of 2 isochoric and 2 isobaric processes. The cycle is clockwise.

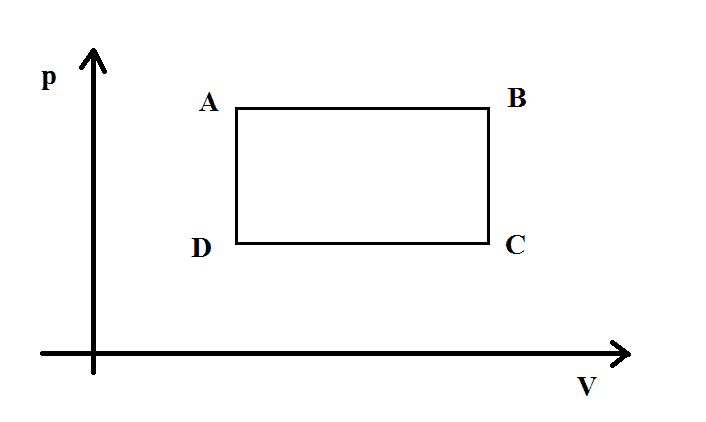
The efficiency is $$\eta=1+\frac{|Q_{C->D}+Q_{B->C}|}{Q_{A->B}+Q_{D->A}}=1+\frac{|c_p(T_{D}-T_{C})+c_v(T_{C}-T_{B})|}{c_p(T_{B}-T_{A})+c_v(T_{A}-T_{D})}\tag{I}$$

Consider the two following cases

1. All the processes in the diagram are reversible
2. One of more of the processes is not reversible

Does $\eta$ changes between case 1 and 2?

On the one hand my answer would be no, as said before, because heats are all functions of temperatures only.

On the other hand this does not makes sense, because Carnot theorem requires that in case 1 (all processes reversible) the efficiency is the same of a Carnot engine working betweeen highest and lowest temperature (in this case $T_{D}$ and $T_{B}$), that is, in case one, $$\eta=1-\frac{T_D}{T_B}\tag{II}$$
Which is not equal to $(I)$.

To sum up, it seems to me that, in this case, $\eta$ does not depend on the reversibility of the engine. I don't see this dipendence which of course is there, because of Carnot theorem. So how does $\eta$ depend of the reversibility of processes in this one case?

Thanks a lot in advice

 

[Let'sthink]

There are some issues of understanding here. We need to find the formula for efficiency for this engine with reversible process. Carnot theorem has two aspects
:1. No engine working between the same two temperatures of reservoirs can have more efficiency than the carnot engine.
2. Two engines working between the same two temperature reservoirs one reversible and the other reversible, the efficiency of the reversible engine engine will be always greater than that of the irreversible engine.
3. The efficiency formula for Carnot engine cannot be lifted as such and applied here. That formula gives efficiency of Carnot engine only.
The concept of reversibility here is not limited to the starting and end state of working substance or environment but is applicable to every infinitesimal part of the process. Once you represent a process on indicator diagram. in principle the process is reversible but actual exchanges of heat between working substance or sink will not be reversible. For example you may think that the heat taken from the source will be as per your formula and will be equal to the increase of internal energy and work done. But it will not be so. Heat taken from the source will be more that this to make up for loss to the environment and also the isobaric process of increase of temperature will not take place infinitely slow as required by the formula to work.
Think along these lines to sharpen your skills about the concepts involved.

 

[Philip Koeck]

A related question: A Carnot engine running between two temperatures Tc and Th has the efficiency 1-Tc/Th. According to a corollary of Carnot’s theorem (see for example Blundell's book) all reversible engines running between Tc and Th would have the same efficiency. However if I calculate the efficiency for an engine with two isotherms at Tc and Th which are connected by either isobars or isochors I get an efficiency lower than that of the Carnot process unless I let the compression ratio become infinite. How do I resolve this contradiction?

 

[Chandra Prayaga]

I calculated the efficiency of the (reversible, non-Carnot) with the two isochores as mentioned above by Philip Koeck, and I am getting exactly the Carnot efficiency. I uploaded the word document showing the calculation.

 

[Philip Koeck]

Hi Chandra. According to textbooks, as far as I know, the efficiency is given by the work done in one cycle divided by the heat entering the system per cycle. In your drawing heat enters the system in steps D to A and A to B. You effectively ignore the heat entering in D to A so D to A might as well be adiabatic. That's why you get the same efficiency as for the Carnot process. At least that's my understanding.

 

[Chestermiller]

Please describe what happens in an adiabatic isobaric irreversible expansion or compression. How is an irreversible adiabatic isobaric expansion or compression defined and implemented?

 

[Chandra Prayaga]

Hi Chandra. According to textbooks, as far as I know, the efficiency is given by the work done in one cycle divided by the heat entering the system per cycle. In your drawing heat enters the system in steps D to A and A to B. You effectively ignore the heat entering in D to A so D to A might as well be adiabatic. That's why you get the same efficiency as for the Carnot process. At least that's my understanding.

Heat entering the system in D to A is not ignored in my calculation. It is exactly equal to (but opposite in sign) to the heat entering the system in B to C. Please check equations (4) and (7).

 

[Philip Koeck]

Hi Chandra. I said "effctively ignored". You balance the heat entering in D to A with the heat leaving in B to C. Why don't you then partly balance the heat entering in A to B with the heat leaving in C to D? If you did that you would find that the net Q is equal to W for one cycle, as it should be for a cyclic process, and your efficiency would be 1. I would say that efficiency is defined as the ratio between W and heat entering. Heat only enters in D to A and A to B. You shouldn't include the negative heat for B to C in calculating the efficiency.

 

[Philip Koeck]

Dear Chestermiller: I don't understand your question. What do you mean by adiabatic isobaric process?

 

[Philip Koeck]

Hi again Chandra. I've had another look at your calculation and I see that you actually state Qnet = Wnet.
The problem that I see is your definition of Qh, which is only the heat entering in A to B in your calculation.
In my opinion you should replace Qh by Qin which would be the sum of the Q for A to B and the Q for D to A.
At least that's how I understand the definition of efficiency.

 

[Chestermiller]

Dear Chestermiller: I don't understand your question. What do you mean by adiabatic isobaric process?

An isobaric process without any heat being added.

Would you consider the following irreversible process isobaric? You have a gas in a cylinder with a piston and weights on top, and vacuum outside. Initially, the system is in equilibrium. You suddenly remove some of the weight from the piston, and let the gas expand spontaneously against the reduced (constant) pressure force exerted by the piston and weights.

 

[Philip Koeck]

Dear Chestermiller. I don't think I would. The pressure of the gas is not constant. It's a bit like a free expansion.

 

[Chestermiller]

Dear Chestermiller. I don't think I would. The pressure of the gas is not constant. It's a bit like a free expansion.

It's a matter of terminology, but many people would refer to this as an irreversible isobaric expansion, even though there was a sudden drop in pressure at the piston face at the beginning. If the piston height re-equilibrated at the end of the expansion, the amount of work done by the gas at the piston face would be $P^*\Delta V$, where $P^*=\frac{Mg}{A}$ and M is the reduced mass of piston and weights.

 

[Philip Koeck]

Okay, I can accept that.

 

[Chestermiller]

Okay, I can accept that.

Do you see how my question relates to reversibility vs irreversibility for a close cycle that involves isobaric segments?

 

[Philip Koeck]

Not sure. Are you saying that an adiabatic isobaric process has to be irreversible and therefore a cycle containing an isobar has to be irreversible?

 

[Chestermiller]

Not sure. Are you saying that an adiabatic isobaric process has to be irreversible and therefore a cycle containing an isobar has to be irreversible?

Yes. A cycle containing an adiabatic isobar has to be irreversible.

 

[Philip Koeck]

What about if the isobar is not adiabatic? Could it then be reversible?

 

[Chestermiller]

What about if the isobar is not adiabatic? Could it then be reversible?

Yes. You would have to do the expansion or compression very gradually, and increase or decrease the temperature in proportion to the increase in volume (using, say, a continuous set of thermal reservoirs).

 

[Philip Koeck]

Okay, I think that answers my question. That really means that a reversible cyclic process consisting of isotherms and isobars between two thermal reservoirs is not possible. The same would be true for a cyclic process consisting of isotherms and isochors. The only processes that can be reversible without this construction of a series of thermal baths are the isotherm and the adiabat. Therefore the Carnot process is really the only cyclic process between two heat baths that can be reversible. This means that this corollary in Blundell actually only says that all Carnot engines with the same temperatures have the same efficiency. That's actually clear as soon as we've worked out that the efficiency only depends on the temperatures. My feeling is Blundell+Blundell should remove this corollary from their textbook or state clearly how little it actually says. Any comments are welcome.

 

[Chestermiller]

Okay, I think that answers my question. That really means that a reversible cyclic process consisting of isotherms and isobars between two thermal reservoirs is not possible. The same would be true for a cyclic process consisting of isotherms and isochors. The only processes that can be reversible without this construction of a series of thermal baths are the isotherm and the adiabat. Therefore the Carnot process is really the only cyclic process between two heat baths that can be reversible. This means that this corollary in Blundell actually only says that all Carnot engines with the same temperatures have the same efficiency. That's actually clear as soon as we've worked out that the efficiency only depends on the temperatures. My feeling is Blundell+Blundell should remove this corollary from their textbook or state clearly how little it actually says. Any comments are welcome.

I'm not familiar with this book, but maybe they mean that, irrespective of the volume changes for the isothermal segments, all Carnot engines with the same temperatures have the same efficiency.

 

[DrClaude]

However if I calculate the efficiency for an engine with two isotherms at Tc and Th which are connected by either isobars or isochors I get an efficiency lower than that of the Carnot process unless I let the compression ratio become infinite. How do I resolve this contradiction?

Using two isochors, you get the cycle for Stirling's engine. For a perfect heat exchanger, you get exactly the calculation @Chandra Prayaga did, resulting in the same efficiency as the Carnot cycle.

 

[Chestermiller]

Using two isochors, you get the cycle for Stirling's engine. For a perfect heat exchanger, you get exactly the calculation @Chandra Prayaga did, resulting in the same efficiency as the Carnot cycle.

This is not operating between two temperatures. There is heat being absorbed or expelled during the isochoric temperature changes, so there are multiple temperatures along the isochores.

 

[Philip Koeck]

Dear Dr. Claude and Chestermiller. In Chandra's calculation the heat entering the system is given as the heat entering during the isotherm at Th. However, as also pointed out by Chestermiller, heat also enters during the isochoric pressure increase. I would say that the sum of these input-heats has to be used when calculating the efficiency. The logical definition of efficiency must be work divided by total heat supplied. Let's get this straight before the next exam period!

 

[Chestermiller]

Dear Dr. Claude and Chestermiller. In Chandra's calculation the heat entering the system is given as the heat entering during the isotherm at Th. However, as also pointed out by Chestermiller, heat also enters during the isochoric pressure increase. I would say that the sum of these input-heats has to be used when calculating the efficiency. The logical definition of efficiency must be work divided by total heat supplied. Let's get this straight before the next exam period!

I can't help to straighten it out, because I see no practical value in doing so.

 

[Chestermiller]

I can't help to straighten it out, because I see no practical value in doing so.

Second thoughts. The isochoric legs of this cycle involve no net heat transfer to or from hot reservoirs or cold reservoirs, and involve no work. So they can be neglected in determining the efficiency of this particular cycle.

 

[Philip Koeck]

How is effiency of a heat engine defined in general then? How would you calculate the efficiency of an Otto-engine (2 adiabats, 2 isochors)?

 

[Chestermiller]

How is effiency of a heat engine defined in general then? How would you calculate the efficiency of an Otto-engine (2 adiabats, 2 isochors)?

The only definition I've ever seen is the work divided by the heat in. For an otto cycle, the efficiency is equal to the net work done during the adiabats divided by the heat input during the high temperature isochor.

 

[Philip Koeck]

Then for the Stirling engine (2 isotherms, 2 isochors) the heat input should be the heat for the high temperature isotherm plus the heat for the isochoric pressure increase. Is that correct?

 

[Chestermiller]

Then for the Stirling engine (2 isotherms, 2 isochors) the heat input should be the heat for the high temperature isotherm plus the heat for the isochoric pressure increase. Is that correct?

Yes.

 

[Philip Koeck]

So you can't neglect the isochoric leg on the left in Chandra's drawing after all.

 

[Chestermiller]

So you can't neglect the isochoric leg on the left in Chandra's drawing after all.

Well, I would, but that's just my own personal judgment call.

 

[Philip Koeck]

To wrap this up: I've found another discussion of the efficiency of the Sterling cycle:
https://physics.stackexchange.com/questions/78915/efficiency-of-stirling-engine-and-carnots-theorem
Might be helpful.

 

[Philip Koeck]

Hi again.
I got a paper via another discussion forum (Research Gate). I don't seem to be able to upload it, though. It's the following paper:
A Simple Approach to Heat Engine Efficiency
Carl Salter (2000)
Journal of Chemical Education 77(8), pp. 1027 -1030

Highly recommended reading. Might help to resolve the controversy in the literature on how to calculate efficiencies.