Temprature-Entropy cyclic process

[astrozilla]

Homework Statement

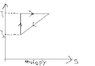
There is a temperature-Entropy graph (T-S) (attachment),which illustrates a hypothetical cyclic process.
a) Calculate the heat input or output along each of the paths.

b) Find an expression for the efficiency η of the complete cycle in terms of T1 and T2 only.

Homework Equations

for b ,η=(Q1/Q2)-1=(T1/T2 )-1,HEAT INPUT: DH=DQ (ONLY in case of isobaric change)

The Attempt at a Solution

 

[physicsworks]

[PLAIN]http://img202.imageshack.us/img202/3227/temperatureentropygragh.jpg
I suppose the most complicated path is the linear process II-III (see attached image) in which both T and S change:
T(S)= \alpha S + T_0
where \alpha, T_0 >0 are some constants.
So, in this process we have
\frac{dS}{dT} = \frac{1}{\alpha}
and hence
\delta Q_{II-III} = TdS = \frac{1}{\alpha} T dT

When T changes from T_1 to T_2 you have
Q_{II-III} = \frac{1}{\alpha}\int_{T_1}^{T_2} TdT = -\frac{1}{2\alpha} \left(T_1^2 - T_2^2 \right)
That is, the heat is extracted in this process.
Now for the process III-I where the entropy is constant it is trivial that Q_{III-I}=0. It is in fact an adiabatic process.

Try to find the heat for isothermal process I-II. Note that the change of the entropy
S_{II} - S_{I}
you can express in terms of T_2, T_1 and \alpha just from the following equations for III and II points on the graph:
T_2 = \alpha S_{I} +T_0

T_1 = \alpha S_{II} + T_0
Note also that S_{I}=S_{III}

 

[astrozilla]

That's amazing.Thank you very much for both answers !