Tension and Friction Problem, I'm finding weird answer.

[tomas_xc]

Homework Statement

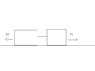
Two blocks A and B are connected by an ideal rope R, both blocks lie on a horizontal surface S. The coefficient of static friction (\mu_s = 0.30) and kinetic friction (\mu_k = 0.20) between the blocks and the surface S are the same for both blocks. The mass of block A is m_A = 6.12 kg. The mass of block B is m_B = 7.51 kg. A horizontal force F_1 = 50.39 N pushes the block A, a horizontal force F_2 = 26.81 N pushes the block B.
Assume g = 9.8 m/s^2.
(See picture)

What is the acceleration of the block and the tension on the rope?

Homework Equations

F = ma
f_k = \mu_k F_n
f_s(max) = \mu_s F_n

The Attempt at a Solution

Since m_A = 6.12 kg, then F_n(A) = 6.12 \times 9.8 = 59.98 N
Since m_B = 7.51 kg, then F_n(B) = 7.51 \times 9.8 = 73.60 N

F_1 is greater than f_s(max), therefore the system is in motion and the friction is kinetic.
f_k(A) = 0.2 \times 59.98 = 12.00 N
f_k(B) = 0.2 \times 73.60 = 14.72 N

Let the direction of F_1 be the positive one, and T be the tension magnitude.
So by Newton's Second Law, we have:
F_1 - f_k(A) - T = m_A \times a
T - F_2 - f_k(B) = m_B \times a

Adding the two equations above yields:
F_1 - F_2 - f_k(A) - f_k(B) = (m_A + m_B) \times a

a = \frac{F_1 - F_2 - f_k(A) - f_k(B)}{m_A + m_B}

a = \frac{50.39 - 26.81 - 12.00 - 14.72}{6.12 + 7.51} = -0.23 m/s^2

But why this negative acceleration? Clearly my answer is wrong, since I assumed the positive direction the direction of F_1, which is greater than F_2. Please, help me.

 

[LowlyPion]

I can't see your picture as yet.

Your equations indicate that the forces are in opposite directions?

If that is the case, then the total static friction that needs to be overcome is (6.12 + 7.51)*9.8*.3 = 40N.

But the net of the 2 forces is 50.39 - 26.81?

Is that the right idea of the problem?

 

[tomas_xc]

Yes, the forces are in opposite directions. Hum, but the correct thing to do is consider the blocks as a unique block and to add all the friction forces? And then decide if the net force is greater than friction?

 

[LowlyPion]

Yes, the forces are in opposite directions. Hum, but the correct thing to do is consider the blocks as a unique block and to add all the friction forces? And then decide if the net force is greater than friction?

You can consider them in isolation too.

For Block A friction is .3*9.8*6.12. That's 18N.
For Block B friction is .3*9.8*7.51. That's 22N

Remember that Static friction is ±. It resists equally in either direction. i.e. it's not conservative. It is available to resist in whatever direction there is a net force. (Of course it does not add as a motive force, it is merely a maximum available force of resistance.)

But to figure out whether the system itself is in motion, isn't it a good idea to determine if the net of the actual forces can overcome the total resistance available?

 

[LowlyPion]

To determine the Tension consider the block with the greater force and the net force required to maintain it in position after accounting for friction. What must the tension be?

 

[tomas_xc]

But I should consider the maximum static friction force for the blocks?
Well, assuming it for the first leads:

f_s(max)(A) = \mu_s F_n(A) = 0.30 \times 59.98 = 17.99 \, N

By Newton's Second Law
F_1 - T - f_s(max)(A) = 0 (Since we assume there's no motion)
50.39 - T - 17.99 = 0
T = 32.40 \, N

But then, on the second block we must have:
F_2 + f(B) - T = 0 (where f(B) is the friction on block B)
26.81 + f(B) - 32.40 = 0
f(B) = 5.59 \, N

But why then the friction on block B is not the maximum static friction? Is there anything that leads us to choose block A as having the maximum static friction? Is necessary that at least one of the blocks have maximum static friction?

For instance, if we consider the block B as having the maximum static friction and then determine the tension and friction on block A, we get:

f_s(max)(B) = \mu_s F_n(B) = 0.30 \times 73.60 = 22.08 \, N

By Newton's Second Law:
T - F_2 - f_s(max)(B) = 0
T = F_2 + f_s(max)(B) = 26.81 + 22.08 = 48.89 \, N

Now we get the friction for body A:
F_1 - T - f(A) = 0
f(A) = F_1 - T = 50.39 - 48.89 = 1.50 \, N

Well, if block B has maximum static friction, the force of friction on block A is not the maximum static friction, but the situation still makes sense.

Following my assumption that the system is not in motion, in general leads:
F_1 - T - f(A) = 0
T - F_2 - f(B) = 0

Adding up the two equations:
F_1 - F_2 - f(A) - f(B) = 0
50.39 - 26.81 = f(A) + f(B)
f(A) + f(B) = 23.58 \, N

This last equation shows us that any two values of f(A) and f(B) satisfying it will satisfy my model of no motion on the system.

But now I ask:
If it is a model of the real world, why I couldn't find just one value for each of the friction forces (and consequently just one value for the tension), but instead several values were found?
Doesn't the forces on the blocks, masses of the blocks, gravity acceleration and friction coefficients completely and uniquely determine the tension and friction forces on the blocks?

Could somebody please help me?
Thanks.

Obs.: I added up a new image with all the forces (except normal force and weight).

 

[LowlyPion]

I would look at it this way.

If it is a static system, then the system would be equivalent to a system that has no force on the smaller side and only the net in the larger side, wouldn't it?

In this case, rather than having 50.39N you would have just 23.6N acting to the left and 0 to the right.

That would mean then that Block B only could supply resistance of friction to the tension, if needed.

Now consider the forces on A. There is the net of 23.6 acting and up to 18N of static friction resistance that would be used up, necessarily first, I would think, until Tension was required to keep it static. Now since friction from Block B is not really an active force in the sense that it would do anything but resist tension up to its limit, then the only tension it would supply would be the tension necessary to keep A static.

In this case that would be 5.6N.

Add that to the original force from the lesser of the forces in the problem, 5.6 + 26.8 problem, yields the 32.4N that is the surplus needed over the 50.4N - 18N = 32.4N.

 

[tomas_xc]

I would look at it this way.

If it is a static system, then the system would be equivalent to a system that has no force on the smaller side and only the net in the larger side, wouldn't it?

In this case, rather than having 50.39N you would have just 23.6N acting to the left and 0 to the right.

But by doing so wouldn't we be raising the friction on block B, since in the new system just the tension (which needs to be the same on the two equivalent systems) acts on the block B?

After finding the tension on the new equivalent system, if we move back to the old one and keep the tension the same, then the friction on block B wouldn't change?

I wonder if the system mentioned above is in some way just tension-equivalent?
Thanks for the reply.

 

[LowlyPion]

I wonder if the system mentioned above is in some way just tension-equivalent?
Thanks for the reply.

If by tension equivalent ... you mean the tension is a pass through of the force from the lesser side. Because I see it as that plus whatever tension is needed to maintain the greater side in equilibrium.

Remember the side with the lesser acting force has no benefit from friction resisting it, because that force must act in the same direction as the lesser force to maintain the static system in the face of the superior force from the other direction.