Tension and Pulley Madness (Load weight)

[jegues]

Homework Statement

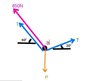
See figure.

Homework Equations

Sum of Fy = 0
Sum of Fx = 0
Tension is constant across the cord, regardless of the number of pulleys.

The Attempt at a Solution

My first thought after looking at the B A E connection to load P was that the hypotenuse of the 60 degree triangle must be 850 Newtons since tension is constant across the rope. Is there any flaws in my reasoning? (I can't seem to get the correct answer so there must be )



Also doesn't the tension in the cord ABCD depend on load P as well? The heaver P is, the greather the tension in the cord will have to be to keep the cord-pulley system from moving. I'm not sure what forces I'm suppose to use to obtain a tension across ABCD.



Any help is greatly appreciated.

 

[tiny-tim]

Hi jegues!

My first thought after looking at the B A E connection to load P was that the hypotenuse of the 60 degree triangle must be 850 Newtons since tension is constant across the rope. Is there any flaws in my reasoning? (I can't seem to get the correct answer so there must be )

There are two ropes between A and B.

Yes, 850 N is the tension in one rope.

But you still have a tension T in the other rope (along AB) (this is like that other thread of yours), and the same tension T along the rope BC.

Try again. ​

 

[jegues]

Here's my attempt at a FBD, is this correct?

EDIT: AHA! Got it ;)

$$F_{x} :$$

$$-(850 + T)cos60 + Tcos30 = 0$$

$$T = 1161.2N$$

$$F_{y} :$$

$$(850 + T)sin60 + Tsin30 - P = 0$$

$$P = 2322.24N$$

 

[tiny-tim]

Excellent!

 

[scienceroks]

how do you measure tension on a catapult because I'm doing a science project and i don't know how